Ядро (теория категорий)

Ядро в теории категорий — категорный эквивалент ядра гомоморфизма из общей алгебры; интуитивно, ядро морфизма $f\colon X\to Y$ — это «наиболее общий» морфизм $k\colon K\to X$ , после которого применение $f$ даёт нулевой морфизм.

Определение

Пусть ${\mathcal {C}}$ — категория с нулевыми морфизмами. Тогда ядро морфизма $f\colon X\to Y$ — это уравнитель его и нулевого морфизма $0\colon X\to Y$ . Более явно, выполняется следующее универсальное свойство:

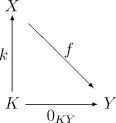
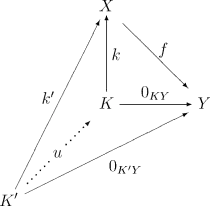
Ядро $f\colon X\to Y$ — это морфизм $k\colon K\to X$ , такой что:

$f\circ k$ — нулевой морфизм из $K$ в $Y$ :

для любого морфизма $k'\colon K'\to X$ , такого что $f\circ k'$ — нулевой, существует единственный морфизм $u\colon K'\to K$ , такой что $k\circ u=k'$ :

Примеры

Во многих категориях это определение ядра совпадает с обычным: если $f\colon X\to Y$ — гомоморфизм групп или модулей, то ядро в категорном смысле — это вложение ядра в алгебраическом смысле в прообраз.

Однако в категории моноидов ядра в категорном смысле аналогичны ядрам групп, поэтому определение ядра в теории моноидов немного отличается. В категории колец, наоборот, ядер в категорном смысле не существует вовсе, так как не существует нулевых морфизмов. Интерпретировать ядра моноидов и колец в теории категорий можно при помощи концепции пар ядер.

Связь с другими категорными понятиями

Двойственное к ядру понятие — коядро, то есть ядро морфизма — это его коядро в двойственной категории, и наоборот.

Каждое ядро, как и любой другой уравнитель, является мономорфизмом. Обратно, мономорфизм называется нормальным, если он является ядром другого морфизма. Категория называется нормальной, если любой мономорфизм в ней нормален.

В частности, абелевы категории являются нормальными. В этой ситуации, ядро коядра морфизма называется его образом. При этом каждый мономорфизм является своим собственным образом.

Литература

Маклейн С. Категории для работающего математика = Categories for the working mathematician / Пер. с англ. под ред. В. А. Артамонова. — М.: Физматлит, 2004. — 352 с. — ISBN 5-9221-0400-4.

Paolo Aluffi. Algebra: Chapter 0. — 2009. — (Graduate Studies in Mathematics). — ISBN 0-8218-4781-3.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.