Шихаллионский эксперимент

Шихаллионский эксперимент (англ. Schiehallion experiment) — эксперимент XVIII века с целью определения средней плотности Земли. Финансируемый грантом Королевского общества, он был проведён летом 1774 года вокруг шотландской горы Шихаллион в Пертшире. Эксперимент включал измерение крошечного отклонения от вертикали подвеса маятника из-за гравитационного притяжения близлежащей горы. Шихаллион считался идеальным местом после поиска гор-кандидатов благодаря своей изоляции и почти симметричной форме.

Изолированное положение Шихаллона и симметричная форма хорошо подходили для эксперимента.

Эксперимент ранее рассматривался, но отвергался Исааком Ньютоном как практическая демонстрация его теории гравитации; однако группа учёных, в частности Невил Маскелайн — королевский астроном, был убеждён, что эффект можно обнаружить, и взялся за проведение эксперимента. Угол отклонения зависел от относительных плотностей и объёмов Земли и горы: если можно было определить плотность и объём Шихаллиона, то можно было определить и плотность Земли. Эта величина также даст приблизительные значения для других планет, их лун и Солнца, которые ранее были известны только с точки зрения их пропорциональных соотношений.

Предыстория

В центрально-симметричном гравитационном поле Земли отвес маятника располагается вертикально, то есть по направлению к центру Земли. Однако если поблизости находится объект достаточно большой массы, выдающийся над поверхностью, такой как гора (либо подземная область с повышенной плотностью — гравитационная аномалия), её гравитационное притяжение должно немного отклонить отвес маятника от истинного. Изменение угла отвеса относительно известного объекта, например звезды, можно было тщательно измерить на противоположных сторонах горы. Если бы масса горы могла быть установлена независимо от определения её объема и оценки средней плотности её горных пород, то эти значения можно было бы экстраполировать, чтобы получить среднюю плотность Земли и, соответственно, её массу.

Исаак Ньютон рассматривал этот эффект в «Началах»[1], но пессимистично полагал, что любая настоящая гора будет производить слишком малое отклонение для измерения. Он писал, что гравитационные эффекты заметны только в планетарном масштабе[2]. Пессимизм Ньютона был необоснованным: хотя его расчёты предполагали отклонение менее 20 угловых секунд (для идеализированной 5-километровой горы), этот угол, хотя и очень небольшой, был в пределах теоретических возможностей инструментов того времени[3].

Эксперимент по проверке идеи Ньютона предоставил бы подтверждающие доказательства его закона всемирного тяготения, а также оценки массы и плотности Земли. Поскольку массы астрономических объектов были известны только с точки зрения относительных соотношений, масса Земли давала разумные значения для других планет, их лун и Солнца. Данные также позволили определить значение гравитационной постоянной Ньютона G, хотя это и не было целью экспериментаторов; ссылки на значение G появятся в научной литературе только спустя почти сто лет[4].

Выбор горы
Чимборасо, субъект французского эксперимента 1738 года.

Чимборасо, 1738 год

Пара французских астрономов, Пьер Бугер и Шарль Мари де ла Кондамин, были первыми, кто попытался провести эксперимент, проведя свои измерения на вулкане Чимборасо высотой 6268-метров (20 564 футов) в «Real Audiencia of Quito» вице-королевства Перу в 1738 году (на территории нынешней провинции Чимборасо в Республике Эквадор)[5]. Их экспедиция отправилась из Франции в Южную Америку в 1735 году, чтобы попытаться измерить длину дуги меридиана в один градус широты вблизи экватора, но они воспользовались возможностью, чтобы попытаться провести эксперимент с отклонением маятника. В декабре 1738 году в очень сложных условиях местности и климата они провели пару измерений на высотах 4680 и 4340 м . Бугер писал в статье 1749 года, что им удалось обнаружить отклонение на 8 секунд дуги, но он преуменьшил значение их результатов, предполагая, что эксперимент лучше проводить в более лёгких условиях во Франции или Англии[3][6]. Он добавил, что эксперимент, по крайней мере, доказал, что Земля не может быть полой оболочкой, как предполагали некоторые мыслители того времени, в том числе Эдмонд Галлей[5].

Шихаллион, 1774 год
Симметричный хребет Шихаллион, вид через Лох-Раннох.

Между 1763 и 1767 годами во время операций по исследованию линии Мейсона — Диксона между штатами Пенсильвания и Мэриленд британские астрономы обнаружили гораздо больше систематических и неслучайных ошибок в своих измерениях, чем можно было ожидать, что продлило работу на более длинный срок, чем планировалось[7]. Когда эта информация дошла до членов Королевского общества, Генри Кавендиш понял, что это явление могло быть связано с гравитационным притяжением близлежащих гор Аллегейни, которое, вероятно, отклонило отвесные линии теодолитов и жидкости внутри спиртовых уровней[8].

Вдохновлённая этой новостью, Невил Маскелин, королевский астроном, предложил Королевскому обществу повторить эксперимент по определению массы Земли в 1772 году[9]. Он предположил, что эксперимент «сделает честь нации, которая его выполнит»[3] и предложил гору Уэрнсайд в Йоркшире, или гору Бленката в массиве Скиддо массив в графстве Камберленд в качестве подходящих целей. Королевское общество сформировало Комитет по привлечению для рассмотрения этого вопроса, назначив Маскелина, Джозефа Бэнкса и Бенджамина Франклина среди его членов[10]. Комитет отправил астронома и геодезиста Чарльза Мейсона найти подходящую гору[1].

После продолжительных поисков летом 1773 года Мейсон сообщил, что лучшим кандидатом был Шихаллон (тогда он назывался Schehallien), пик, лежащий между озерами Лох-ей и Лох-Раннох в центральном Северо-Шотландском нагорье[10]. Гора стояла изолированно от любых близлежащих холмов, что уменьшало их гравитационное влияние, а её симметричные восточный и западный гребни упрощали расчёты. Его крутые северный и южный склоны позволили бы провести эксперимент близко к его центру масс, максимизировав эффект отклонения. По совпадению, вершина находится почти точно в центре Шотландии по широте и долготе[11].

Мейсон отказался выполнять работу сам за предложенную комиссию в одну гинею в день[10]. Поэтому эта задача выпала на долю Маскелина, за что ему был предоставлен временный отпуск с должности Королевского астронома. Ему помогали в этой задаче математик и геодезист Чарльз Хаттон и Ройбен Бёрроу — математик из Королевской Гринвичской обсерватории. Для строительства обсерваторий для астрономов и оказания помощи в съёмке была привлечена рабочая сила. Научная группа была особенно хорошо оснащена: её астрономические инструменты включали латунный квадрант из экспедиции Кука по прохождению Венеры 1769 года, а также зенитный телескоп и регулятор (точные маятниковые часы) для хронометража астрономических наблюдений[12]. Они также приобрели теодолит и цепь Гюнтера для съёмки горы и пару барометров для измерения высоты[12]. Щедрое финансирование эксперимента было доступно из-за недорасхода на экспедицию по наблюдению транзита Венеры по диску Солнца, которая была поручена Обществу королём Георгом III[1][3].

Измерения

Астрономические
Отклонение — это разница между истинным зенитом Z как определено астрометрией, и видимым зенитом Z′ как определено по отвесу.

К северу и югу от горы были построены обсерватории, а также помещение для размещения оборудования и учёных. Руины этих построек остались на склоне горы. Большая часть рабочей силы размещалась в грубых брезентовых палатках. Астрономические измерения Маскелина провели первыми. Ему было необходимо определить зенитные расстояния по линии отвеса для набора звёзд в точное время, когда каждая из них проходила строго на юг (астрономическую широту)[3][13]. Погодные условия часто были неблагоприятными из-за тумана и дождя. Однако из южной обсерватории ему удалось провести 76 измерений 34 звёзд в одном направлении, а затем 93 наблюдения 39 звёзд в другом. Затем с северной стороны он провёл серию из 68 наблюдений за 32 звёздами и серию из 100 наблюдений за 37 звёздами[6]. Проведя серию измерений с плоскостью зенитного сектора, обращённой сначала на восток, а затем на запад, он успешно избежал каких-либо систематических ошибок, возникающих при коллимации сектора[1].

Чтобы определить отклонение из-за присутствия горы, необходимо было учесть кривизну Земли: наблюдатель, движущийся на север или юг, увидит смещение местного зенита на тот же угол, что и любое изменение геодезической широты. После учёта наблюдаемых эффектов, таких как прецессия, аберрация света и нутация, Маскелин показал, что разница между локально определённым зенитом для наблюдателей к северу и югу от Шихаллиона составляет 54,6 угловые секунды. После того, как геодезическая группа предоставила разницу в 42,94″ широты между двумя станциями, он смог вычесть это и после округления до точности своих наблюдений объявить, что сумма северного и южного отклонений составляет 11,6″[3][6][14].

Маскелин опубликовал свои первоначальные результаты в Philosophical Transactions of the Royal Society в 1775 году[14], используя предварительные данные о форме горы и, следовательно, о положении её центра тяжести. Это заставило его ожидать отклонения в 20,9″, если бы средние плотности Шихаллиона и Земли были равны[3][15]. Поскольку отклонение было примерно вдвое меньше, он смог сделать предварительное заявление о том, что средняя плотность Земли примерно вдвое больше, чем у Шихаллиона. Для получения более точного значения необходимо дождаться завершения процесса съемки[14].

Маскелин воспользовался возможностью, чтобы отметить, что Шихаллион проявлял гравитационное притяжение, и, таким образом, все горы; и что ньютоновский закон обратных квадратов всемирного тяготения был подтверждён[14]. Благодарное Королевское общество вручило Маскелину медаль Копли 1775 года; биограф Чалмерс позже заметил, что «если ещё оставались какие-то сомнения относительно истинности ньютоновской системы, теперь они полностью устранены».

Геодезия

Работе геодезической группы сильно мешала ненастная погода, и на выполнение задачи ушло время до 1776 года[15][К 1]. Чтобы найти объём горы, нужно было разделить её на набор вертикальных призм и вычислить объём каждой. Задача триангуляции, выпавшая на долю Чарльза Хаттона, была серьёзной: геодезисты получили тысячи пеленгов более чем в тысяче точек вокруг горы[17]. К тому же вершины его призм не всегда удобно совпадали с измеряемыми высотами. Чтобы разобраться во всех своих данных, ему пришла в голову идея интерполировать серию линий через заданные интервалы между его измеренными значениями, отмечая точки одинаковой высоты. При этом он не только мог легко определить высоту своих призм, но и по завихрениям линий можно было получить мгновенное представление о форме местности. Таким образом, Хаттон использовал контурные линии, которые стали широко использоваться с тех пор для изображения картографического рельефа[17].

Таблица плотности Солнечной системы Хаттона
Тело Плотность, кг·м −3
Хаттон, 1778 г.[18][К 2] Современное значение[19]
Солнце 1100 1408
Меркурий 9200 5427
Венера 5800 5204
Земля 4500 5515
Луна 3100 3340
Марс 3300 3934
Юпитер 1100 1326
Сатурн 410 687

Хаттон должен был вычислить индивидуальное притяжение для каждой из множества призм, образующих его сетку, процесс, который был таким же трудоёмким, как и само исследование. Эта задача отняла у него ещё два года, прежде чем он смог представить свои результаты, что он и сделал в стостраничной статье для Королевского общества в 1778 году[18]. Он обнаружил, что притяжение отвеса к Земле было бы в 9933 раза больше, чем сумма его притяжений к горе на северной и южной станциях, если бы плотность Земли и Шихаллиона была одинаковой[17]. Поскольку фактическое отклонение в 11,6″ подразумевало соотношение 17 804:1 после учёта влияния широты на гравитацию, он смог заявить, что Земля имеет среднюю плотность , или около плотности горы[15][17][18]. Таким образом, длительный процесс обследования горы не сильно повлиял на результаты расчётов Маскелина. Хаттон взял плотность годы 2,500 кг·м−3 и объявил, что плотность Земли равна из них, или 4,500 кг·м−3[17]. По сравнению с принятой в настоящее время цифрой 5,515 кг·м−3[19] плотность Земли вычислена с погрешностью менее 20 %.

То, что средняя плотность Земли должна настолько сильно превышать плотность её поверхностных пород, естественно, означало, что более плотный материал должен лежать глубже. Хаттон правильно предположил, что материал ядра, вероятно, был металлическим и мог иметь плотность 10,000 кг·м−3[17]. По его оценке, эта металлическая часть занимает около 65 % диаметра Земли[18]. Имея значение средней плотности Земли, Хаттон смог установить некоторые значения для планетарных таблиц Жерома Лаланда, которые ранее могли выражать плотности только основных объектов Солнечной системы в относительных единицах[18].

Последующие эксперименты

Более точное измерение средней плотности Земли было сделано через 24 года после Шихаллиона, когда в 1798 году Генри Кавендиш использовал исключительно чувствительные крутильные весы для измерения притяжения между большими шарами свинца. Цифра Кавендиша 5,448 ± 33 кг·м−3 отличалась всего на 1,2 % от принятого в настоящее время значения 5,515 кг·м−3, и его результат не будет значительно улучшен вплоть до 1895 года в измерениях Чарльза Бойса[К 3]. Тщательность, с которой Кавендиш провёл эксперимент, и точность его результатов привели к тому, что с тех пор его имя стало ассоциироваться с первым измерением плотность Земли[21].

Джон Плейфэр провёл второе обследование Шихаллиона в 1811 году; на основе переосмысления пластов горных пород он предложил плотность от 4560 до 4,870 кг·м−3[22], хотя тогдашний пожилой Хаттон энергично отстаивал первоначальное значение в статье 1821 года для Общества[3][23]. Расчёты Плейфэра приблизили плотность к её современному значению, но всё ещё были слишком низкими и значительно хуже, чем расчёты Кавендиша несколькими годами ранее.

Трон Артура — место проведения эксперимента Генри Джеймса 1856 года.

Шихаллионский эксперимент был повторен в 1856 году Генри Джеймсом — генеральным директором Топографической службы, который вместо горы использовал холм Трон Артура в центре Эдинбурга[24]. Имея в своём распоряжении ресурсы Службы артиллерийского вооружения, Джеймс расширил свою топографическую съемку до 21-километрового радиуса, доведя его до границ Мидлотиана. Он получил плотность около 5,300 кг·м−3[3][15].

В эксперименте 2005 года был предпринят повторить работы 1774 года: вместо вычисления локальных различий в зените в эксперименте было проведено очень точное сравнение периода маятника вверху и внизу Шихаллона. Период маятника зависит от g, местного ускорения силы тяжести. Ожидалось, что маятник будет двигаться медленнее на высоте, но масса горы уменьшит эту разницу. Этот опыт имеет то преимущество, что его значительно легче провести, чем опыт 1774 года, но для достижения желаемой точности необходимо измерить период маятника с точностью до одной миллионной доли[13]. Этот эксперимент дал значение массы Земли 8.1 ± 2.4 × 1024 кг[25], что соответствует средней плотности 7,500 ± 1,900 кг·м−3[К 4]. 

Современная повторная проверка геофизических данных позволила учесть факторы, которые группа 1774 года не смогла учесть. Благодаря цифровой модели рельефа радиусом 120 км, значительному расширению знаний о геологии Шихаллиона и помощи компьютера в отчёте 2007 г. была получена средняя плотность Земли 5,480 ± 250 кг·м−3[26]. По сравнению с современной цифрой 5,515 кг·м−3 это свидетельствует о точности астрономических наблюдений Маскелина[26].

Математическая процедура
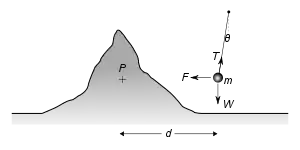
Диаграмма силы, действующая со стороны Шихаллиона на маятник.

Рассмотрим силовую диаграмму справа, на которой отклонение сильно преувеличено. Анализ был упрощён за счёт рассмотрения притяжения только с одной стороны горы[22]. Отвес массы m находится на расстоянии d от P, центр масс горы MM и плотность ρM. Он отклоняется на небольшой угол θ из-за его притяжения F к P и его веса W направленного к Земле. Векторная сумма W и F приводит к натяжению T в струне маятника. Земля имеет массу ME, радиус rE и плотность ρE[22].

Две гравитационные силы, действующие на отвес, определяются законом всемирного тяготения Ньютона:

где G — гравитационная постоянная Ньютона. G и m можно исключить, взяв отношение F к W:

где VM и VE — объёмы горы и Земли. При статическом равновесии горизонтальная и вертикальная составляющие натяжения струны T может быть связана с гравитационными силами и углом отклонения θ:

Подставляя T :

Поскольку VE, VM и rE известны, θ измерено и d вычислено, то значение отношения ρE : ρM можно получить в виде[22]:

Комментарии
  1. Во время пьяной вечеринки, посвящённой окончанию съемки, северная обсерватория случайно сгорела дотла, забрав с собой скрипку, принадлежавшую Дункану Робертсону, младшему члену исследовательской группы. В благодарность за развлечение, которое игра Робертсона доставляла Маскелину в течение четырёх месяцев астрономических наблюдений, он компенсировал его, заменив потерянную скрипку той, которая теперь называется The Yellow London Lady[16].
  2. Значения Хаттона выражаются в виде обыкновенных дробей, кратных плотности воды, например, для Марса . Здесь они выражены как целое число из двух значащих цифр, умноженное на плотность воды 1000 кг·м−3[18].
  3. Значение 5,480 кг·м−3 появляется в статье Кавердиша. Однако он допустил арифметическую ошибку: его измерения фактически привели к значению 5,448 кг·м−3; несоответствие, которое было обнаружено в 1821 года Фрэнсисом Бейли[20].
  4. Приняв объем Земли за 1.0832 × 1012 км3[13].

Примечания
  1. Davies, R.D. (1985). “A Commemoration of Maskelyne at Schiehallion”. Quarterly Journal of the Royal Astronomical Society. 26 (3): 289—294. Bibcode:1985QJRAS..26..289D.
  2. Newton, Isaac. Philosophiæ Naturalis Principia Mathematica. — 1972. — Vol. II. — P. 528. — ISBN 0-521-07647-1. (недоступная ссылка) Translated: Andrew Motte, First American Edition. New York, 1846
  3. Sillitto. Maskelyne on Schiehallion: A Lecture to The Royal Philosophical Society of Glasgow (31 October 1990). Дата обращения: 28 декабря 2008.
  4. Cornu, A. (1873). “Mutual determination of the constant of attraction and the mean density of the earth”. Comptes rendus de l'Académie des sciences. 76: 954—958.
  5. Poynting, J.H. The Earth: its shape, size, weight and spin. — Cambridge, 1913. — P. 50–56.
  6. Poynting, J. H. The mean density of the earth. — 1894. — P. 12–22.
  7. Mentzer, Robert (August 2003). “How Mason & Dixon Ran Their Line” (PDF). Professional Surveyor Magazine. Дата обращения 3 August 2021.
  8. Tretkoff. This Month in Physics History June 1798: Cavendish weighs the world. American Physical Society. Дата обращения: 3 августа 2021.
  9. Maskelyne, N. (1772). “A proposal for measuring the attraction of some hill in this Kingdom”. Philosophical Transactions of the Royal Society. 65: 495—499. Bibcode:1775RSPT...65..495M. DOI:10.1098/rstl.1775.0049.
  10. Danson, Edwin. Weighing the World. — Oxford University Press, 2006. — P. 115–116. — ISBN 978-0-19-518169-2.
  11. Hewitt, Rachel. Map of a Nation: A Biography of the Ordnance Survey. — Granta Books, 2010. — ISBN 9781847084521.
  12. Danson, Edwin. Weighing the World. — Oxford University Press, 2006. — P. 146. — ISBN 978-0-19-518169-2.
  13. The "Weigh the World" Challenge 2005. countingthoughts (23 April 2005). Дата обращения: 28 декабря 2008.
  14. Maskelyne, N. (1775). “An Account of Observations Made on the Mountain Schiehallion for Finding Its Attraction”. Philosophical Transactions of the Royal Society. 65: 500—542. DOI:10.1098/rstl.1775.0050.
  15. Poynting, J. H. A text-book of physics / J. H. Poynting, Thomson, J. J.. — 1909. — P. 33–35. — ISBN 1-4067-7316-6.
  16. The Yellow London Lady (англ.). Clan Donnachaidh Society. Дата обращения: 19 февраля 2022.
  17. Danson, Edwin. Weighing the World. — Oxford University Press, 2006. — P. 153–154. — ISBN 978-0-19-518169-2.
  18. Hutton, C. (1778). “An Account of the Calculations Made from the Survey and Measures Taken at Schehallien”. Philosophical Transactions of the Royal Society. 68. DOI:10.1098/rstl.1778.0034.
  19. Planetary Fact Sheet. Lunar and Planetary Science. NASA. Дата обращения: 2 января 2009.
  20. Falconer, Isobel (1999). “Henry Cavendish: the man and the measurement”. Measurement Science and Technology. 10 (6): 470—477. Bibcode:1999MeScT..10..470F. DOI:10.1088/0957-0233/10/6/310.
  21. Jungnickel, Christa. Cavendish / Christa Jungnickel, Russell McCormmach. — American Philosophical Society, 1996. — P. 340–341. — ISBN 978-0-87169-220-7.
  22. Ranalli, G. (1984). “An Early Geophysical Estimate of the Mean Density of the Earth: Schehallien, 1774”. Earth Sciences History. 3 (2): 149—152. DOI:10.17704/eshi.3.2.k43q522gtt440172.
  23. Hutton, Charles (1821). “On the mean density of the earth”. Proceedings of the Royal Society.
  24. James (1856). “On the Deflection of the Plumb-Line at Arthur's Seat, and the Mean Specific Gravity of the Earth”. Proceedings of the Royal Society. 146: 591—606. DOI:10.1098/rstl.1856.0029.
  25. The "Weigh the World" Challenge Results. countingthoughts. Дата обращения: 28 декабря 2008.
  26. Smallwood, J.R. (2007). “Maskelyne's 1774 Schiehallion experiment revisited”. Scottish Journal of Geology. 43 (1): 15—31. DOI:10.1144/sjg43010015.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.