Релятивистская механика

Область применения релятивистской механики

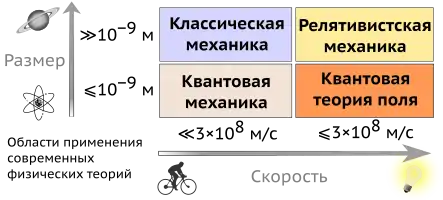
В классической механике пространственные координаты и время являются независимыми (при отсутствии гомоных связей, зависящих от времени), время является абсолютным, то есть течёт одинаково во всех системах отсчёта, и действуют преобразования Галилея. В релятивистской же механике события происходят в четырёхмерном пространстве, объединяющем физическое трёхмерное пространство и время (пространство Минковского) и действуют преобразования Лоренца. Таким образом, в отличие от классической механики, одновременность событий зависит от выбора системы отсчёта.

Основные законы релятивистской механики — релятивистское обобщение второго закона Ньютона и релятивистский закон сохранения энергии-импульса — являются следствием такого «смешения» пространственных и временной координат при преобразованиях Лоренца.

Сила определяется как

${\displaystyle {\vec {F}}={\frac {d{\vec {p}}}{dt}}.}$

Также известно выражение для релятивистского импульса:

${\displaystyle {\vec {p}}={\frac {m{\vec {v}}}{\sqrt {1-v^{2}/c^{2}}}}.}$

Взяв для определения силы производную по времени от последнего выражения, получим:

${\displaystyle {\frac {d{\vec {p}}}{dt}}=m\gamma {\vec {a}}+m\gamma ^{3}{\vec {\beta }}({\vec {\beta }}{\vec {a}}),}$

где введены обозначения: ${\displaystyle {\vec {\beta }}\equiv {\frac {\vec {v}}{c}}}$ и ${\displaystyle \gamma \equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}}}$.

В результате выражение для силы приобретает вид:

${\displaystyle {\vec {F}}=m\gamma {\vec {a}}+m\gamma ^{3}{\vec {\beta }}({\vec {\beta }}{\vec {a}}).}$

Отсюда видно, что в релятивистской механике в отличие от нерелятивистского случая ускорение не обязательно направлено по силе, в общем случае ускорение имеет также и составляющую, направленную по скорости.

Запишем интеграл действия, исходя из принципа наименьшего действия

${\displaystyle S=-\int \limits _{a}^{b}\alpha ds,}$

где ${\displaystyle \alpha }$-положительное число. Как известно из специальной теории относительности (СТО)

${\displaystyle ds=c{\sqrt {1-v^{2}/c^{2}}}dt.}$

Подставляя в интеграл движения, находим

${\displaystyle S=-\int \limits _{t_{1}}^{t_{2}}\alpha c{\sqrt {1-v^{2}/c^{2}}}dt.}$

Но, с другой стороны, интеграл движения, можно выразить через функцию Лагранжа

${\displaystyle S=\int \limits _{t_{1}}^{t_{2}}{\mathcal {L}}dt.}$

Сравнивая последние два выражения, нетрудно понять, что подынтегральные выражения должны быть равны, то есть

${\displaystyle {\mathcal {L}}=-\alpha c{\sqrt {1-v^{2}/c^{2}}}.}$

Далее, разложим последнее выражение по степеням ${\displaystyle {\frac {v}{c}}}$, получим

${\displaystyle {\mathcal {L}}\simeq \alpha c+{\frac {\alpha v^{2}}{2c}}.}$

Первый член разложения не зависит от скорости, а значит не вносит никаких изменений в уравнения движения. Тогда, сравнивая с классическим выражением функции Лагранжа: ${\displaystyle {\frac {mv^{2}}{2}}}$, нетрудно определить константу ${\displaystyle \alpha }$

${\displaystyle \alpha =mc.}$

Таким образом, окончательно получаем вид функции Лагранжа свободной частицы

${\displaystyle {\mathcal {L}}=-mc^{2}{\sqrt {1-v^{2}/c^{2}}}.}$

Рассуждения, приведенные выше, можно рассматривать не только для частицы, но и для произвольного тела, лишь бы его части двигались как одно целое.

Поскольку квадрат 4-вектора импульса ${\displaystyle P_{\alpha }}$ является постоянной величиной:

${\displaystyle P_{\alpha }P^{\alpha }-m^{2}c^{2}=0,}$

то релятивистская частица может рассматриваться как механическая система с неголономной связью в 4-мерном псевдоевклидовом пространстве[1][2][3].

• Теория относительности
• Специальная теория относительности
• Общая теория относительности
• Релятивистски равноускоренное движение
• Релятивистская электродинамика

• Паули В. Теория относительности. М.: Наука, 1991. 328 с.
• Принцип относительности. Сборник работ по специальной теории относительности. М.: Атомиздат, 1973.
• Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 3-е, переработанное. — М.: Физматгиз, 1960. — 512 с. — («Теоретическая физика», том II).
• Уиттекер Э. История теории эфира и электричества. Современные теории 1900—1926. Пер с англ. Москва, Ижевск: ИКИ, 2004. 464с. ISBN 5-93972-304-7 (Глава 2)