Резонанс Гельмгольца

Для описания процесса колебаний в резонаторе Гельмгольца хорошо подходит акусто-механическая аналогия описывающая колеблющийся под действием возмущений газ в горле резонатора сосредоточенной массой и сопротивлением (демпфером), а деформируемый в объёме резонатора газ сосредоточенной упругостью. Совокупность массы, сопротивления и упругости образует классический механический колебательный контур типа "груз на пружинке" обладающий резонансной (собственной) частотой колебаний. Резонансная частота колебаний резонатора Гельмгольца главным образом зависит от размера и формы горла и объёма полости. Как и в любом другом колебательном контуре колебания в резонаторе Гельмгольца могут проявляться в виде автоколебаний или вынужденных колебаний. Пример автоколебаний — гудение пустой бутылки от потока воздуха направленного перпендикулярно её горлышку. Вынужденные колебания — та же бутылка, но без потока и с приходящими к ней извне акустическими возмущениями.

Модель резонатора Гельмгольца

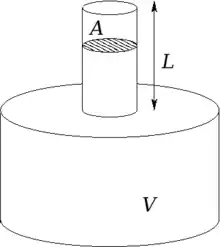
Может быть показано[2] что собственная угловая частота колебаний равна

${\displaystyle \omega _{\text{H}}={\sqrt {\gamma {\frac {A^{2}}{m}}{\frac {P_{0}}{V_{0}}}}},}$

где ${\displaystyle \gamma }$ — показатель адиабаты, значение которого обычно равно 1,4 для воздуха и двуатомных газов; ${\displaystyle A}$ — площадь сечения горлышка; ${\displaystyle m}$ — масса воздуха в горлышке; ${\displaystyle P_{0}}$ — статическое давление в полости; ${\displaystyle V_{0}}$ — статический объём полости.

Для цилиндрических горлышек

${\displaystyle A={\frac {V_{n}}{L}},}$

где: ${\displaystyle L}$ — длина горлышка, ${\displaystyle V_{n}}$ — объём воздуха в горлышке, поэтому

${\displaystyle \omega _{\text{H}}={\sqrt {\gamma {\frac {A}{m}}{\frac {V_{n}}{L}}{\frac {P_{0}}{V_{0}}}}}.}$

По определению плотности:

${\displaystyle {\frac {V_{n}}{m}}={\frac {1}{\rho }},}$

поэтому

${\displaystyle \omega _{\text{H}}={\sqrt {\gamma {\frac {P_{0}}{\rho }}{\frac {A}{V_{0}L}}}},}$

и

${\displaystyle f_{\text{H}}={\frac {\omega _{H}}{2\pi }},}$

где ${\displaystyle f_{H}}$ — резонансная частота.

Скорость звука в газах равна

${\displaystyle v={\sqrt {\gamma {\frac {P_{0}}{\rho }}}},}$

поэтому можно выразить резонансную частоту через неё:

${\displaystyle f_{\text{H}}={\frac {v}{2\pi }}{\sqrt {\frac {A}{V_{0}L}}}.}$

Длина горлышка появляется в знаменателе потому, что инерция воздуха в горлышке пропорциональна массе воздуха в горлышке, а значит, и длине. Объём появляется в знаменателе потому, что коэффициент сжимаемости воздуха в полости обратно пропорционален объёму. Площадь сечения горлышка влияет двояко — чем больше площадь, тем больше масса воздуха в горлышке, и тем меньше скорость, с которой воздух устремляется внутрь и вовне.

Эта формула имеет границы применимости, зависящие от формы горлышка и толщины стенок резонатора. Исходя из примерно такой же физической модели можно получить более точную формулу[3]. Кроме этого, если скорость потока рядом с резонатором высока (более 0,3 числа Маха), необходимо вводить дополнительные поправки.

Резонанс Гельмгольца применяется в двигателях внутреннего сгорания и в акустических системах. Системы впрыска топлива, называемые системами Гельмгольца, использовались в двигателях Chrysler V10, которыми комплектовались автомобили Dodge Viper и пикапы Ram, а также в мотоциклах Buell.

В струнных инструментах с полой декой, таких, как гитара или скрипка, один из пиков кривой резонанса — это резонанс Гельмгольца (остальные — это резонансные частоты деревянных частей инструмента). Окарина — резонатор с изменяемым сечением горлышка. Западноафриканский барабан джембе имеет относительно узкое горлышко, что придаёт ему глубокий басовый тон. Джаг — классический резонатор Гельмгольца.

Теория резонанса Гельмгольца используется при проектировании выхлопных труб автомобилей и мотоциклов, с целью сделать звук двигателя более тихим или более красивым.

• Hermann von Helmholtz. On the sensations of tone as a physiological basis for the theory of music / Alexander John Ellis. — Longmans, Green, 1885. — 576 с.
• Колебания и волны. Лекции. В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев (Физический факультет МГУ) Издательство Физического факультета МГУ, 2001 г.

• Oxford Physics Teaching, History Archive, «Exhibit 3 — Helmholtz resonators Архивная копия от 26 декабря 2020 на Wayback Machine» (archival photograph)
• HyperPhysics Acoustic Laboratory
• HyperPhysics Cavity Resonance
• Beverage Bottles as Helmholtz Resonators // Science Project Idea for Students
• Helmholtz Resonance