Полярная окружность

Полярная окружность треугольника — это окружность, центр которой совпадает с ортоцентром треугольника, а радиус равен

${\displaystyle {\begin{aligned}r^{2}&=HA\times HD=HB\times HE=HC\times HF\\&=-4R^{2}\cos A\cos B\cos C=4R^{2}-{\frac {1}{2}}(a^{2}+b^{2}+c^{2}),\end{aligned}}}$

Полярная окружность

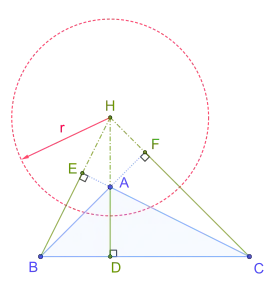
где A, B, C означают как вершины, так и соответствующие углы, а точка H — ортоцентр (пересечение высот). Точки D, E и F являются основаниями высот, опущенных из вершин A, B и C соответственно, R является радиусом описанной окружности, а a, b и c — длинами сторон треугольника, противоположных вершинам A, B и C соответственно[1].

Первая часть формулы отражает факт, что ортоцентр делит высоты на отрезки, произведения которых равны. Тригонометрическая часть формулы показывает, что полярный круг существует только в случае, когда треугольник является тупоугольным, так что один из косинусов отрицателен.