Пластичность (физика)
Пласти́чность — способность материала без разрушения получать большие остаточные деформации. Свойство пластичности имеет решающее значение для таких технологических операций, как штамповка, вытяжка, волочение, изгиб и др. Мерой пластичности являются относительное удлинение и относительное сужение , определяемые при проведении испытаний на растяжение. Чем больше , тем более пластичным считается материал. По уровню относительного сужения можно делать вывод о технологичности материала. К числу весьма пластичных материалов относятся отожженная медь, алюминий, латунь, золото, малоуглеродистая сталь и др. Менее пластичными являются дюраль и бронза. К числу слабо пластичных материалов относятся многие легированные стали.
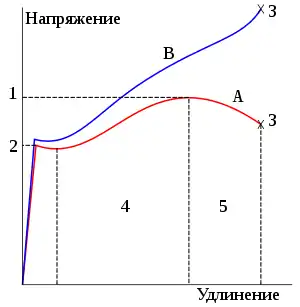
1 — Предел прочности.
2 — Предел текучести (предел упругости).
3 — Точка разрушения.
4 — Область деформационного упрочнения.
5 — Область формирования шейки.
A: Видимое напряжение ().
B: Истинное напряжение ().
—исходное сечение недеформированного образца;
—текущее сечение образца под напряжением.
У пластичных материалов прочностные характеристики на растяжение и сжатие сопоставляют по пределу текучести. Принято считать, что т.р≈т.с.
Деление материалов на пластичные и хрупкие является условным не только потому, что между теми и другими не существует резкого перехода в значениях и . В зависимости от условий испытания многие хрупкие материалы способны вести себя как пластичные, а пластичные — как хрупкие.
Очень большое влияние на проявление свойств пластичности и хрупкости оказывают скорость натяжения и температура. При быстром натяжении более резко проявляется свойство хрупкости, а при медленном — свойство пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки при нормальной температуре получать остаточные деформации. Пластичные же материалы, такие как малоуглеродистая сталь, под воздействием резкой ударной нагрузки проявляют хрупкие свойства.
Физические механизмы

В металлах
Пластичность кристалла чистого металла в первую очередь обусловлена двумя режимами деформации кристаллической решетки: скольжением и двойникованием. Скольжение — это деформация сдвига, которая перемещает атомы относительно их начального положения на расстояния существенно большие чем межатомные расстояния. Двойникование — это пластическая деформация, которая происходит вдоль плоскости в результате чего происходит поворот части кристалла.
Большинство металлов в горячем состоянии более пластичны, чем в холодном состоянии. Свинец показывает достаточную пластичность при комнатной температуре, в то время как чугун не демонстрирует достаточной пластичности для любых операциях ковки, даже в горячем состоянии. Это свойство важно при операциях формования и экструзии металлов. Большинство металлов приобретают пластичность при нагревании и, следовательно, в горячем состоянии.
Системы скольжения
Кристаллические материалы содержат однородные плоскости атомов, обладающие дальним порядком. Плоскости могут скользить друг относительно друга в направлениях с плотной упаковкой. В результате происходит постоянное изменение формы кристалла и пластическая деформация. Наличие дислокаций увеличивает вероятность появления таких плоскостей.
Обратимая пластичность
На наномасштабе первичная пластическая деформация в простых гранецентрированных кубических металлах обратима, если отсутствует перенос материала в виде поперечного скольжения[1].
Микропластичность — это локальное явление в неоднородных металлах. Оно возникает при механических напряжениях, когда металл в целом находится в упругой области, но некоторые локальные области находятся в пластической области[2].
Трещинообразование
В аморфных материалах, в отсутствие дальнего порядка, понятие «дислокаций» неприменимо, поскольку весь материал лишен дальнего порядка. Эти материалы все ещё могут подвергаться пластической деформации. Поскольку аморфные материалы, такие как полимеры, неупорядочены, то они содержат большое количество свободного объёма. Вытягивание таких материалов с натяжением открывает эти области и может привести к помутнению материала. Эта матовость является результатом образования множества трещин, когда внутри материала образуются фибриллы в областях с высоким объёмным напряжением. Внешний вид материала может измениться от упорядоченного до рисунка с цеком (англ. crazing) в виде напряжений и растяжек.
Ячеистые материалы
Ячеистые материалы деформируются пластически, когда изгибающий момент превышает пластический момент. Это относится к пенопластам с открытыми ячейками, где изгибающий момент действует на стенки ячеек. Пены могут быть изготовлены из любого материала с пределом пластической текучести, включая жесткие полимеры и металлы. Этот метод моделирования пены в виде балок действителен только в том случае, если отношение плотности пены к плотности вещества меньше 0,3. Это связано с тем, что балки испытывают пластические деформации в осевом направлении, а не изгибаются. В пенопластах с закрытыми порами предел текучести увеличивается, если материал находится под напряжением растяжения из-за мембраны, которая охватывает поверхность ячеек.
Почвы и песок
Грунты, особенно глины, проявляют значительную неупругость под действием нагрузки. Причины пластичности почв могут быть довольно сложными и сильно зависят от их микроструктуры, химического состава и содержания воды. Пластичность почвы вызвана в первую очередь перестройкой скоплений соседних зерен.
Камни и бетон
Неупругие деформации горных пород и бетона в первую очередь вызываются образованием микротрещин и скольжением относительно этих трещин. При высоких температурах и давлениях на пластическое поведение также может влиять движение дислокаций в отдельных зернах микроструктуры.
Математические описания
Теория деформации
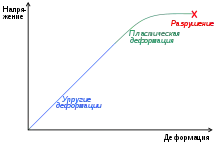
Есть несколько модельных математических описаний пластичности[3]. Одно из них — теория деформаций (см., Например, Закон Гука), где тензор напряжений Коши (ранга d−1 в d-мерном пространстве) является функцией тензора деформации. Хотя это описание является точным, когда небольшая часть тела подвергается возрастающей нагрузке (например, деформационной нагрузке), эта теория не может объяснить необратимость.
Пластичные материалы могут выдерживать большие пластические деформации без разрушения (потери сплошности). Однако даже пластичные металлы будут разрушаться, когда деформация станет достаточно большой — это происходит в результате деформационного упрочнения материала, в результате чего он становится хрупким. Термическая обработка, такая как отжиг, может восстановить пластичность обрабатываемой детали, для продолжения формования.
Теория пластического течения
В 1934 году Эгон Орован, Майкл Поланьи и Джеффри Ингрэм Тейлор примерно одновременно предложили рассматривать пластическую деформацию некоторых материалов с помощью теории дислокаций. Математическая теория пластичности, теория пластического течения, использует набор нелинейных, неинтегрируемых уравнений для описания набора изменений деформации и напряжения по сравнению с предыдущим состоянием и небольшого увеличения деформации.
Предел текучести
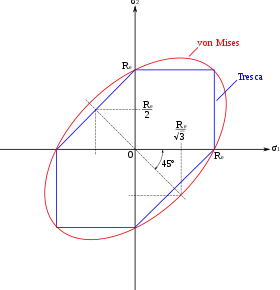
Если напряжение превышает критическое значение (предел текучести), материал подвергнется пластической или необратимой деформации. Это критическое напряжение может быть растягивающим или сжимающим. Критерии Треска́ и фон Мизеса обычно используются для определения того, течёт ли материал. Однако эти критерии оказались неадекватными для значительно количества материалов, и несколько других критериев текучести также получили широкое распространение.
Критерий Треска
Критерий Треска основан на представлении о том, что при каком-то напряжении с материалом происходят необратимые изменения, например, из-за сдвига. Это является хорошим предположением при рассмотрении металлов. Учитывая основное напряженное состояние, можно использовать круг Мора для определения максимальных касательных напряжений, и сделать вывод, что материал выйдет потечёт, если
где σ 1 — максимальное нормальное напряжение, σ 3 — минимальное нормальное напряжение, а σ 0 — напряжение, при котором материал течёт одноосном нагружении. Можно построить поверхность текучести, которая дает визуальное представление об этой концепции. Внутри поверхности текучести деформация упругая (не обязательно линейная). На поверхности возникает пластическая деформация. Материал не может иметь напряженное состояние за пределами своей поверхности текучести.
Критерий Губера — фон Мизеса
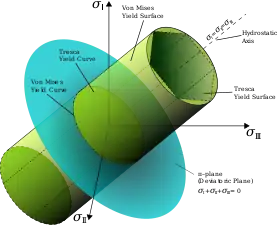
Критерий Губера — фон Мизеса[4] основан на критерии Трески, но учитывает предположение, что гидростатическое напряжение не способствует разрушению материала. М. Т. Губер был первым, кто предложил использовать критерий сдвиговой энергии[5][6]. Фон Мизес нашёл эффективное напряжение при одноосном нагружении, вычитая главные напряжения, и постулирует, что все эффективные напряжения, превышающие то, которое вызывает текучесть материала при одноосном нагружении, приведут к пластической деформации:
Визуальное представление поверхности текучести можно построить с использованием приведенного выше уравнения, которое принимает форму эллипса. Внутри поверхности материалы подвергаются упругой деформации. Достижение поверхности означает, что материал подвергается пластической деформации.
Примечания
- Gerolf Ziegenhain and Herbert M. Urbassek: Reversible Plasticity in fcc metals. In: Philosophical Magazine Letters. 89(11):717-723, 2009 DOI
- Maaß, R. (January 2018). “Micro-plasticity and recent insights from intermittent and small-scale plasticity”. Acta Materialia. 143: 338—363. arXiv:1704.07297. DOI:10.1016/j.actamat.2017.06.023.
- Hill, R. The Mathematical Theory of Plasticity. — Oxford University Press, 1998. — ISBN 0-19-850367-9.
- von Mises, R. (1913). “Mechanik der festen Körper im plastisch-deformablen Zustand”. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. 1913 (1): 582—592.
- Huber, M. T. (1904). “Właściwa praca odkształcenia jako miara wytezenia materiału”. Czasopismo Techniczne. Lwów. 22. Translated as “Specific Work of Strain as a Measure of Material Effort”. Archives of Mechanics. 56: 173—190. 2004.
- See Timoshenko, S. P. History of Strength of Materials. — New York : McGraw-Hill, 1953. — P. 369. — ISBN 9780486611877.
См. также
Литература
- Феодосьев В. И. Сопротивление материалов. — М.: Изд-во МГТУ им. Н. Э. Баумана, 1999. С. 86. ISBN 5-7038-1340-9
- Малинин Н. Н. Прикладная теория пластичности и ползучести. - М., Машиностроение, 1968. - 400 с.