Параллактический треугольник

Параллактический треугольник (навигационный треугольник, PZX-треугольник) — в астронавигации сферический треугольник на небесной сфере, вершинами которого являются полюс (P), зенит (Z), и какое-либо выбранное светило (X). Другими словами, параллактический треугольник образован взаимным пересечением небесного меридиана, круга высоты и круга склонения.

Сторонами треугольника служат дуги PZ = 90° - φ, ZR = z и PR = 90° - δ, где φ — широта на которой находится наблюдатель, z — зенитное расстояние светила, а δ — его склонение.

Углы треугольника в свою очередь: при вершине Z = 180° — A, где A — это азимут, при вершине P = t, то есть равен часовому углу и третий угол, при светиле R, обозначается q и называется параллактический угол[1].

Конфигурация параллактического треугольника зависит от широты, на которой находится наблюдатель, и от времени.

Применение

Решение параллактического треугольника позволяет определить координаты места наблюдения, а также рассчитать моменты времени восхода и захода светил применительно к месту наблюдения, азимуты светил при восходе и заходе, определить местное звёздное время.

Астрономические треугольники

Частными случаями параллактических треугольников являются астрономические треугольники, используемые для перехода между различными системами сферических координат, используемых в астрономии при помощи формул сферической тригонометрии.

Первый астрономический треугольник используется для перевода координат из первой экваториальной системы в горизонтальную и обратно.

Второй астрономический треугольник используется для перевода координат из второй экваториальной системы в эклиптическую и обратно.

Третий астрономический треугольник используется для перевода координат из второй экваториальной системы в галактическую и обратно.

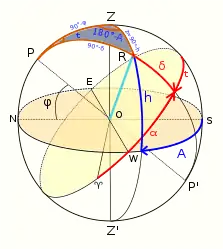Первый астрономический треугольник PZR
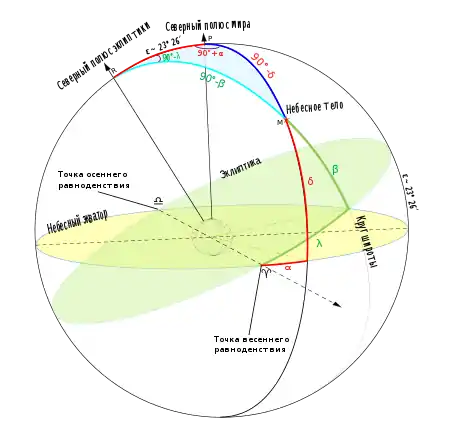Второй астрономический треугольник RPM
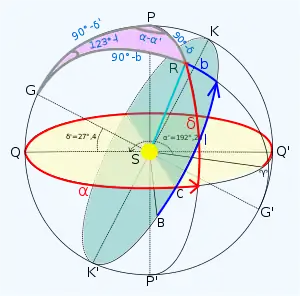Третий астрономический треугольник GPR

Примечания

Попов П. И., Баев К. Л., Воронцов-Вельяминов Б. А., Куницкий Р. В. §19 Параллактический треугольник. Преобразование координат. // Астрономия. — четвёртое. — М.: Учпедгиз, 1958. — С. 57 — 60. — 462 с.

Ссылки

В.Е. Жаров. 3.5. Преобразование координат из одной системы в другую // Сферическая астрономия.
Параллактический треугольник // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Параллактический треугольник — статья из Большой советской энциклопедии.
www.bibliotekar.ru //Параллактический треугольник и преобразование координат.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Попов П. И., Баев К. Л., Воронцов-Вельяминов Б. А., Куницкий Р. В. §19 Параллактический треугольник. Преобразование координат. // Астрономия. — четвёртое. — М.: Учпедгиз, 1958. — С. 57 — 60. — 462 с.