Осцилляции Фриделя
Осцилляции Фриделя[1] — периодическое распределение электронной плотности, возникающее при экранировании электрического заряда дефекта.[2] Названы в честь французского физика Жака Фриделя. Возникают вследствие локализованных возмущений в металлической или полупроводниковой системе, вызванных дефектом в ферми-газе или ферми-жидкости .[3]
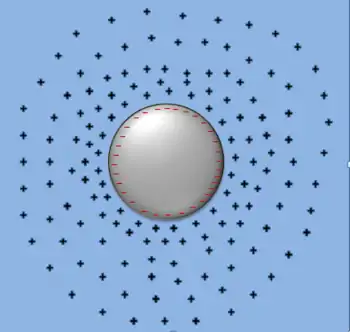
Осцилляция Фриделя является квантовомеханическим аналогом экранирования электрического заряда заряженных частиц в «бассейне» ионов (см. рис. 1). В то время как классическая теория экранирования электрического заряда использует понятие точечных зарядов для описания состава ионного «бассейна», осцилляции Фриделя, описывающие фермионы в ферми — жидкости или ферми — газе, требуют квантового описания рассеяния электронных волн на потенциале дефекта. Такие осцилляции отражают характерное экспоненциальное затухание фермионной плотности вблизи возмущения, за которым следует затухание с осцилляциями (r — расстояние от дефекта).
Рассеяние на дефекте
Электроны, двигающиеся в металле или полупроводнике, подобны свободным электронам с волновой функцией в виде плоской волны, то есть
- .
Электроны в металле ведут себя иначе, чем частицы в обычном газе, поскольку электроны являются фермионами, и они подчиняются статистике Ферми-Дирака. Такое поведение означает, что каждое k - состояние в газе может быть занято только двумя электронами с противоположным спином. Занятые состояния заполняют сферу в зонной структуре k - пространства до фиксированного энергетического уровня — энергии Ферми . Радиус шара в k - пространстве, , называется волновым вектором Ферми, — эффективная масса.
Если в металле или полупроводнике находится чужеродный атом, так называемая примесь, электроны, свободно двигающиеся в проводнике, рассеиваются потенциалом примеси. Поскольку электронный газ является ферми-газом, только электроны с энергиями, близкими к уровню Ферми, могут участвовать в процессе рассеяния, так как должны существовать пустые конечные состояния с близкой энергией, в которые могли бы перейти электроны после рассеяния. Состояния вокруг уровня Ферми занимают ограниченный диапазон k — значений или длин волн. Поэтому только электроны в ограниченном диапазоне длин волн вблизи энергии Ферми рассеиваются, что приводит к модуляции плотности заряда. вокруг примеси. Для сферически симметричного потенциала примеси, имеющей положительный заряд, в трехмерном металле плотность заряда осциллирует, как функция расстояния от примеси. :
- ,
где — орбитальное квантовое число, — фаза рассеяния парциальной компоненты волновой функции электрона, — диэлектрическая проницаемость металла с волновым вектором, равным удвоенному вектору Ферми. Избыточное количество электронов вокруг примесного иона определяется правилом сумм Фриделя:
Для произвольной размерности электронной системы, , добавка к плотности заряда на больших расстояниях от дефекта имеет вид:[4]
Качественное описание
В классическом сценарии экранирования электрического заряда наблюдается затухание электрического поля в заряженной жидкости при наличии заряженного объекта. Поскольку экранирование электрического заряда рассматривает движущиеся заряды в жидкости как точечные объекты, концентрация этих зарядов относительно расстояния от точки уменьшается экспоненциально. Это явление описывается уравнением Пуассона-Больцмана .[5]
Локализованный у дефекта заряд создается быстрыми электронами ферми-газа, которые притягиваются к дефекту, замедляют свое движение возле него и скапливаются в этой области. Существование резкой границы длин электронных волн приводит к возникновению эффектов квантовой интерференции, в результате чего вокруг рассеивающего цента возникает гало заряда.[6]
Примечание. Там, где классически вблизи заряженного возмущения можно наблюдать подавляющее количество противоположно заряженных частиц, в квантовомеханическом сценарии осцилляций Фриделя — это периодическое расположение противоположно заряженных фермионов, за которыми следуют пространства с такими же заряженными областями.[3]
Визуализация двумерных осцилляций

Сканирующая туннельная микроскопия позволяет с атомным разрешением исследовать локальную плотность электронных состояний. (ЛПС) вблизи поверхности проводника:
где — волновая функция электрона с учетом рассеяния на дефекте, — энергия электрона с двумерным волновым вектором , — дельта-функция Дирака.
Рассеяние на дефекте приводит к интерференции волн и изменению плотности состояний, что отражает рассеивающие свойства дефекта.[8] Типичными дефектами поверхности являются адсорбированные инородные единичные атомы (точечные дефекты) и атомные ступени (линейные дефекты) (Рис.2). Одним из способов понимания качественных характеристик стоячих волн у ступенчатого края является приближение, в котором плоский ступенчатый край моделируется непроницаемым барьером для поверхностных электронов. Ступенчатый край создает узел ЛПС, , на грани ступени , а ЛПС на расстоянии от ступени описывается уравнением:[8]
,
где — функция Бесселя первого рода.

Рис. 3 — двумерные осцилляции Фриделя проиллюстрированы СТМ - изображением чистой поверхности, на которой размещены наноостровки кобальта. На изображении хорошо видны двумерные фриделевские осцилляции плотности электронных состояний у точечных дефектов и границ островков.
Ссылки
- http://gravityandlevity.wordpress.com/2009/06/02/friedel-oscillations-wherein-we-learn-that-the-electron-has-a-size/ - простое объяснение этого явления
Примечания
- У. ХАРРИСОН. ТЕОРИЯ ТВЕРДОГО ТЕЛА ИЗДАТЕЛЬСТВО «МИР» МОСКВА 1972
- Фриделя осцилляции. Энциклопедия физики и техники.
- Friedel Oscillations: wherein we learn that the electron has a size. Gravity and Levity (June 2, 2009). Дата обращения: 22 декабря 2009.
- Kai Sotthewes, Michiel Nijmeijer, and Harold J. W. Zandvliet Confined Friedel oscillations on Au(111) terraces probed by thermovoltage scanning tunneling microscopy. PHYSICAL REVIEW B 103, 245311 (2021)
- Hans-Jürgen Butt, Karlheinz Graf, and Michael Kappl, Physics and Chemistry of Interfaces, Wiley-VCH, Weinheim, 2003.
- 'Принципы теории твердого тела'; Займан, Дж.; Изд-во: М.: Мир, 1966
- «Atomic-scale Observations of Alloying at the Cr-Fe(001) Interface» by A. Davies, J.A. Stroscio, D.T. Pierce, and R.J. Celotta, Phys. Rev. Lett. 76, 4175 (1996).
- M. F. Crommie, C. P. Lutz, and D. M. Eigler, Nature (London) 363, 524 (1993); Science 262, 218 (1993).
- Spin mapping at the nanoscale and atomic scale. Roland Wiesendanger. Rev. Mod. Phys. 81, 1495 (2009)