Октодерево
Октодерево (дерево октантов, восьмеричное дерево, англ. octree) — тип древовидной структуры данных, в которой у каждого внутреннего узла ровно восемь «потомков». Восьмеричные деревья чаще всего используются для разделения трёхмерного пространства, рекурсивно разделяя его на восемь ячеек. Октодеревья являются трёхмерными аналогами квадродеревьев. Англоязычное название «octree» сформировано из oct + tree и обычно пишется как «octree», а не «octtree».
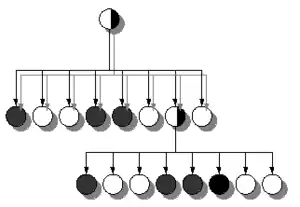
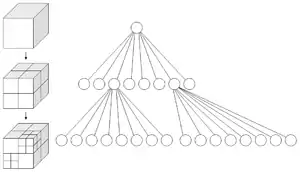
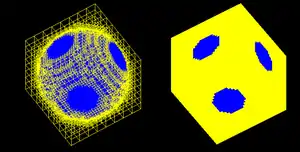
Представление пространства октодеревом
Каждый узел (англ. node) в дереве октантов делит пространство на восемь новых октантов. В региональной точке (англ. point region — PR) октодерева узел сохраняет явную трёхмерную точку, которая является «центром» разделения пространства для этого узла. Данная точка определяет один из углов каждого из восьми дочерних пространств. В MX-октодереве точка разделения является неявным центром пространства, которое представляет узел. Корневой узел PR-октодерева может представлять бесконечное пространство. Корневой узел MX-октодерева должен представлять ограниченную область пространства, так чтобы неявные центры были чётко определёнными. Октодеревья не могут считаться k-мерными деревьями, поскольку k-мерные деревья разделяются вдоль размерности, а октодеревья разделяются вокруг точки. Кроме того, k-мерные деревья всегда являются двоичными, что неверно для октодеревьев.
Общее использование октодеревьев
- Пространственная индексация
- Эффективное обнаружение столкновений в трёхмерном пространстве
- Определение скрытых поверхностей
- Быстрый метод мультиполей
- Неструктурированная сетка
- Метод конечных элементов
- Трассировка лучей
Применение для квантования цвета
Алгоритм октодерева для квантования цвета, изобретённый Гервауцем и Пургатхофером в 1988 году, кодирует данные о цвете изображения как октодерево с девятью уровнями в глубину. Использование октодерева объясняется тем, что и в системе RGB есть три компоненты цвета. Данный алгоритм очень эффективен по отношению к использованию памяти, потому что размер дерева может быть ограничен. Нижний (базовый) уровень октодерева состоит из узловых листьев (англ. leaf nodes), которые накапливают данные о цвете, которые не представлены в дереве; эти узлы первоначально содержат единичные биты. Если в октодерево введено намного большее количество цветовой палитры, чем желательное, то размер октодерева может непрерывно сокращаться, ведя поиск узла на нижнем (базовом) уровне и составляя в среднем его битовые данные в узловой лист, сокращая часть дерева. Как только осуществление выборки закончено, в дереве исследуются все маршруты по направлению вниз к узловым листьям, принимая во внимание биты по пути поиска. Этот процесс приведёт к приблизительному количеству требуемых цветов.
Использование октодеревьев в конкретных приложениях
- Urho3D — свободный игровой движок.
- Sauerbraten — компьютерная игра, которая использует игровой движок Cube 2, который использует октодеревья.
- OGRE — свободный объектно-ориентированный графический движок, в котором присутствует менеджер сцен, использующий октодеревья (англ. Octree Scene Manager)
- Dendro — параллельная мультисеточная библиотека для вычислений методом конечных элементов, использующая октодерево (MPI/C++ реализация)
- FLASH - пакет кодов для численного моделирования астрофизических процессов от Чикагского университета.
Внешние ссылки
- Англоязычные источники
- Octree Quantization в Microsoft Systems Journal
- Квантизация цвета с использованием октодеревьев
- Color Quantization using Octrees in Dr. Dobb's Source Code (недоступная ссылка)
- Обзор октодеревьев
- Parallel implementation of octtree generation algorithm, P. Sojan Lal, A Unnikrishnan, K Poulose Jacob, ICIP 1997, IEEE Digital Library
- Generation of Octrees from Raster Scan with Reduced Information Loss, P. Sojan Lal, A Unnikrishnan, K Poulose Jacob, IASTED International conference VIIP 2001 (недоступная ссылка)
- C++ implementation (GPL license)
- Parallel Octrees for Finite Element Applications Архивная копия от 3 марта 2016 на Wayback Machine
- Русскоязычные источники
- Артем Мерец «Scart». Алгоритм Octree - теория и практика на DirectX 2. UralDev (26 февраля 2007). Дата обращения: 3 июня 2009. Архивировано 2 апреля 2012 года.
- Артем Мерец «Scart». Алгоритм Octree (часть 2) 2. UralDev (5 февраля 2008). Дата обращения: 3 июня 2009. Архивировано 2 апреля 2012 года.
- Джо. Разбиение объектного пространства сцены путём построения octree-дерева. GameDev.ru. Дата обращения: 3 июня 2009.
- Octree (Дерево октантов). GameDev.ru. Дата обращения: 3 июня 2009.
- Алексей Игнатенко. Графический процесс Геометрическое моделирование Лекция 6 (недоступная ссылка). Дата обращения: 3 июня 2009. Архивировано 2 апреля 2012 года.