Односторонний предел

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Определения

Пусть на некотором числовом множестве $M\subset \mathbb {R}$ задана числовая функция $f\colon M\to \mathbb {R}$ и число $a$ — предельная точка области определения $M$ . Существуют различные определения для односторонних пределов функции $f\left(x\right)$ в точке $a$ , но все они эквивалентны.

Односторонний предел по Гейне

Число $A\in \mathbb {R}$ называется правосторонним пределом (правым пределом, пределом справа) функции $f\left(x\right)$ в точке $a$ , если для всякой последовательности $\left\{x_{n}\right\}_{n=1}^{\infty }$ , состоящей из точек, больших числа $a$ , которая сама сходится к числу $a$ , соответствующая последовательность значений функции $\left\{f\left(x_{n}\right)\right\}_{n=1}^{\infty }$ сходится к числу $A$ .
$\lim _{x\to a+0}f\left(x\right)=A\Leftrightarrow \forall \left\{x_{n}\right\}_{n=1}^{\infty }\colon \left(\forall k\in \mathbb {N} \colon x_{k}>a\right)\land \lim _{n\to \infty }x_{n}=a\Rightarrow \lim _{n\to \infty }\left\{f\left(x_{n}\right)\right\}_{n=1}^{\infty }=A$
Число $A\in \mathbb {R}$ называется левосторонним пределом (левым пределом, пределом слева) функции $f\left(x\right)$ в точке $a$ , если для всякой последовательности $\left\{x_{n}\right\}_{n=1}^{\infty }$ , состоящей из точек, меньших числа $a$ , которая сама сходится к числу $a$ , соответствующая последовательность значений функции $\left\{f\left(x_{n}\right)\right\}_{n=1}^{\infty }$ сходится к числу $A$ .[1]
$\lim _{x\to a-0}f\left(x\right)=A\Leftrightarrow \forall \left\{x_{n}\right\}_{n=1}^{\infty }\colon \left(\forall k\in \mathbb {N} \colon x_{k}<a\right)\land \lim _{n\to \infty }x_{n}=a\Rightarrow \lim _{n\to \infty }\left\{f\left(x_{n}\right)\right\}_{n=1}^{\infty }=A$

Односторонний предел по Коши

Число $A\in \mathbb {R}$ называется правосторонним пределом (правым пределом, пределом справа) функции $f\left(x\right)$ в точке $a$ , если для всякого положительного числа $\varepsilon$ отыщется отвечающее ему положительное число $\delta$ такое, что для всех точек $x$ из интервала $\left(a,a+\delta \right)$ справедливо неравенство $\left|f\left(x\right)-A\right|<\varepsilon$ .
$\lim _{x\to a+0}f\left(x\right)=A\Leftrightarrow \forall \varepsilon >0~\exists \delta =\delta \left(\varepsilon \right)>0~\forall x\in \left(a,a+\delta \right)\colon \left|f\left(x\right)-A\right|<\varepsilon$
Число $A\in \mathbb {R}$ называется левосторонним пределом (левым пределом, пределом слева) функции $f\left(x\right)$ в точке $a$ , если для всякого положительного числа $\varepsilon$ отыщется отвечающее ему положительное число $\delta$ , такое, что для всех точек $x$ из интервала $\left(a-\delta ,a\right)$ справедливо неравенство $\left|f\left(x\right)-A\right|<\varepsilon$ .[1]
$\lim _{x\to a-0}f\left(x\right)=A\Leftrightarrow \forall \varepsilon >0~\exists \delta =\delta \left(\varepsilon \right)>0~\forall x\in \left(a-\delta ,a\right)\colon \left|f\left(x\right)-A\right|<\varepsilon$

Односторонний предел как предел вдоль фильтра

Односторонний предел является частным случаем общего понятия предела функции вдоль фильтра. Пусть $M\subset \mathbb {R} ,$ и $a\in M'.$ Тогда системы множеств

{\mathfrak {B}}_{+}=\{(a,a+\delta )\cap M\mid \delta >0\}

и

{\mathfrak {B}}_{-}=\{(a-\delta ,a)\cap M\mid \delta >0\}

являются фильтрами. Пределы вдоль этих фильтров совпадают с соответствующими односторонними пределами:

\lim \limits _{{\mathfrak {B}}_{+}}f(x)\equiv \lim \limits _{x\to a+}f(x);

\lim \limits _{{\mathfrak {B}}_{-}}f(x)\equiv \lim \limits _{x\to a-}f(x).

Обозначения

Правосторонний предел принято обозначать любым из нижеследующих способов:
$\lim \limits _{x\to a+}f(x),\ \ \lim \limits _{x\to a+0}f(x),\ \ \lim _{x\downarrow a}f(x),\ \ \lim _{x\searrow a}f(x);$
Аналогичным образом для левосторонних пределов приняты обозначения:
$\lim \limits _{x\to a-}f(x),\ \ \lim \limits _{x\to a-0}f(x),\ \ \lim _{x\uparrow a}f(x),\ \ \lim _{x\nearrow a}f(x).$
При этом используются также сокращённые обозначения:
- $f\left(a+\right)$ и $f\left(a+0\right)$ для правого предела;
- $f\left(a-\right)$ и $f\left(a-0\right)$ для левого предела.

При $a=0$ для сокращения записи вместо $\lim \limits _{x\to 0+0}f(x)$ и $\lim \limits _{x\to 0-0}f(x)$ обычно пишут $\lim \limits _{x\to +0}f(x)$ и $\lim \limits _{x\to -0}f(x)$ соответственно.

Свойства

Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра.
Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.[1]

Примеры

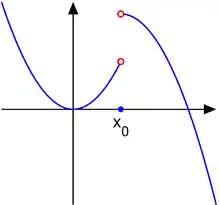
Функция из второго примера

Тождественная числовая функция
- $f\left(x\right)=x$
- Область определения: $\mathbb {R}$
- Правый предел: $\forall a\in \mathbb {R} \colon \lim _{x\to a+0}x=a$
- Левый предел: $\forall a\in \mathbb {R} \colon \lim _{x\to a-0}x=a$
- Правый и левый пределы совпадают, так что имеется обычный предел: $\forall a\in \mathbb {R} \colon \lim _{x\to a}x=a$
Кусочно-заданная функция
- $f\left(x\right)={\begin{cases}x^{2},&x<3\\11-\left(x-3\right)^{2},&x>3\end{cases}}$
- Область определения: $\mathbb {R} \setminus \left\{3\right\}$
- Правый предел: $\lim _{x\to 3+0}f\left(x\right)=11$
- Левый предел: $\lim _{x\to 3-0}f\left(x\right)=9$
- Правый и левый пределы различны, так что обычного предела в точке $x=3$ не существует
Функция sgn(x)
- $f\left(x\right)={\begin{cases}0,&x=0\\{\frac {x}{\left|x\right|}},&x\neq 0\end{cases}}$
- Область определения: $\mathbb {R}$
- Правый предел: $\lim _{x\to 0+0}\operatorname {sgn} \left(x\right)=+1$
- Левый предел: $\lim _{x\to 0-0}\operatorname {sgn} \left(x\right)=-1$
- Правый и левый пределы различны, так что обычного предела в точке $x=0$ не существует

См. также

Предел функции

Примечания

В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 105 — 121. — 672 с. — ISBN 5-482-00445-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[ilyin-1] В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 105 — 121. — 672 с. — ISBN 5-482-00445-7.