Обратимый клеточный автомат
Обратимый клеточный автомат — клеточный автомат, в котором каждое состояние имеет единственного предшественника. Таким образом, это регулярная решётка из ячеек, состояние каждой из которых берётся из конечного множества состояний, и правило для одновременного обновления состояний ячеек, исходя из состояний её соседей. Условие обратимости заключается в том, что предыдущее состояние любой ячейки может быть определено, зная обновлённые состояния всех ячеек решётки. После обращения времени получается другой обратимый клеточный автомат, возможно — с намного большими окрестностями, но также с правилом для определения будущего состояния ячейки, исходя из текущих состояний ей соседей.

Известно несколько методов задания обратимых клеточных автоматов, включая блочные клеточные автоматы, у которых каждый блок обновляется независимо от остальных, и клеточные автоматы второго порядка, в которых правило обновления ячеек определяется двумя предыдущими состояниями автомата. При этом, если автомат задан при помощи таблицы правил, задача проверки его обратимости разрешима для одномерного клеточного автомата, но неразрешима в общем случае.
Обратимые клеточные автоматы задают естественную модель обратимых вычислений — технологии, которая позволяет создать вычислительные устройства с очень низким потреблением электроэнергии. Квантовые клеточные автоматы, которые позволяют производить вычисления с использованием принципов квантовой механики, часто предполагаются обратимыми. Кроме того, многие модели из физики, такие как движение молекул идеального газа или модель Изинга размещения магнитных зарядов, естественным образом обратимы и моделируются обратимым клеточными автоматами.
Свойства, присущие обратимым клеточным автоматам, могут быть использованы для изучения автоматов, которые необратимы, но имеют аттрактор — подмножество состояний, к которому сходятся случайные начальные состояния. Как пишет Стивен Вольфрам, «при приближении к аттрактору любая система, даже необратимая, проявляет некоторые свойства, близкие к обратимости»[1].
Примеры
Элементарные клеточные автоматы
Простейшие клеточные автоматы имеют одномерный массив ячеек, каждая из которых содержит 0 или 1, при том что окрестность ячейки состоит из неё самой и по одному соседу с каждой стороны; такие клеточные автоматы называются элементарными[2]. Если функция перехода никогда не меняет состояние ячейки, всегда заменяет его на противоположное, заменяет его на состояние соседа (всегда одного и того же — слева или справа) или применяет комбинацию из последних двух операций, то такой элементарный клеточный автомат обратим. Несмотря на свою простоту, функция перехода, присваивающая каждой ячейке значение её соседа, играет важную роль в символической динамике, где она известна как оператор сдвига[3].
Элементарные клеточные автоматы необратимы, не считая упомянутых выше тривиальных случаев, в которых каждая ячейка определяется состоянием только одного из своих соседей. Однако близко к обратимым правило 90, в котором будущее состояние каждой ячейки является суммой по модулю 2 (также известным как исключающее «ИЛИ», англ. XOR) текущих состояний её двух соседей. Хотя правило 90 необратимо, каждая его конфигурация имеет ровно четыре предшественника, а также правило 90 локально обратимо, то есть любая последовательность подряд идущих состояний имеет хотя бы одного предшественника[4].
Другие одномерные примеры
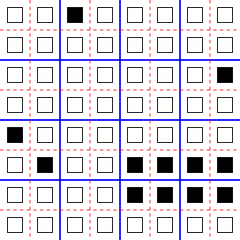
Немного более сложный пример получается так: пусть состояние каждой ячейки является упорядоченной парой (l,r), а функция перехода берёт левую часть нового состояния у соседа слева, а правую — справа. При этом мы предполагаем, что левая и правая части берутся из двух различных конечных множеств возможных значений. Пример изображён на иллюстрации в начале статьи: левая часть состояния — это форма фигуры, а правая — это её цвет. Такой автомат обратим, поскольку можно взять левую часть предыдущего состояния у ячейки справа, а правую — слева.
Другой пример обратимого одномерного клеточного автомата производит умножение на 2 или 5 в десятичной записи. Каждая цифра при таком умножении зависит только от двух предыдущих разрядов, а потому окрестность, определяющая следующее значение, конечна, что и необходимо для клеточного автомата. Вообще говоря, умножение или деление числа в позиционной записи на натуральное число n задаётся клеточным автоматом тогда и только тогда, когда все простые множители числа n входят в основание системы счисления. Такой автомат одномерен и обратим, поскольку можно поделить или умножить соответственно на то же число. И, например, умножение на 3 в десятичной записи не задаётся клеточным автоматом, поскольку может произвойти перенос через сколь угодно большое число разрядов: при умножении 333334*3=1000002 происходит перенос через 5 разрядов[5].
Криттеры

Игра «Жизнь», один из наиболее известных клеточных автоматов, не является обратимым: например, многие конфигурации вымирают. Также в нём существуют Сады Эдема — конфигурации без предшественников. Взамен Томмасо Тоффоли и Норман Марголус изобрели «Криттеров» — обратимый клеточный автомат с динамическим поведением, во многом схожим с «Жизнью»[6].
«Криттеры» — блочный клеточный автомат, в котором ячейки разделены на блоки 2 × 2, обновляющиеся отдельно от остальных. При этом после каждого шага разделение на блоки меняется: они сдвигаются на одну ячейку по горизонтали и вертикали. Функция перехода «Криттеров» меняет состояние каждой ячейки на противоположное, если число живых ячеек в блоке не равняется двум, и вращает на 180° блок целиком, если это число равняется трём. Поскольку число живых ячеек меняется на число мёртвых, а функции перехода при каждом значении числа ячеек обратимы, такой клеточный автомат обратим на каждом блоке, а потому обратим в целом[6].
Если начать с небольшого количества случайных ячеек внутри бо́льшего региона мёртвых ячеек, то из центрального региона распространится много маленьких шаблонов, подобных планеру из игры «Жизнь», которые будут сложным образом взаимодействововать. При этом «Криттеры» допускают сложные космические корабли и осцилляторы с бесконечным числом различных периодов[6].
Конструкции
Известно несколько общих методов построения обратимых клеточных автоматов.
Блочные клеточные автоматы
Блочный клеточный автомат — клеточный автомат, ячейки которого поделены на равные блоки, а функция перехода применяется к каждому блоку по отдельности. Обычно такой автомат по очереди использует несколько разбиений на блоки[7]. Типичным примером такой схемы является окрестность Марголуса, в которой ячейки квадратной решётки поделены на блоки 2 × 2 вертикальными и горизонтальными прямыми, а после каждого шага разделение на блоки сдвигается на одну ячейку по горизонтали и вертикали; таким образом, все четыре ячейки любого блока оказываются в разных блоках на следующем шаге[8]. «Криттеры», рассмотренные выше, используют окрестность Марголуса.
Чтобы блочный клеточный автомат был обратимым, необходимо и достаточно обратимости функции перехода на каждом блоке, что делает возможной проверку обратимости блочного клеточного автомата при помощи полного перебора. При этом обратный клеточный автомат тоже является блочным с такой же структурой разбиений на блоки, но обратной функцией перехода[7].
Моделирование необратимых автоматов
Любой -мерный клеточный автомат можно вложить в -мерный обратимый: при этом каждое состояние нового автомата хранит всю историю эволюции старого. Используя это вложение, Тоффоли показал, что многие свойства необратимых клеточных автоматов переносятся на обратимые, например, они могут быть полны по Тьюрингу[9].
Увеличение размерности в такой конструкции не случайно: при некоторых слабых ограничениях (вроде инвариантности вложения относительно параллельных переносов) доказано, что любое вложение клеточного автомата с «Садом Эдема», то есть конфигурацией без предшественников, в обратимый клеточный автомат должно увеличивать размерность[10].
Однако, при наличии состояний покоя (англ. quiescent states), то есть состояний, которые не меняются при условии, что соседние состояния также не меняются[как?], возможно моделирование конечной конфигурации клеточного автомата в блочном обратимом клеточном автомате той же размерности[11]. Информация, которая должна была бы быть потеряна на следующем шаге, взамен хранится в бесконечном регионе из клеток, находящихся в состоянии покоя. При этом время, необходимое для моделирования части конфигурации, пропорционально её размеру. Тем не менее, такая конструкция позволяет доказать существование обратимого одномерного клеточного автомата, полного по Тьюрингу[12].
Примечания
- Wolfram (2002), p. 1018.
- Schiff (2008), p. 44.
- Blanchard, Devaney & Keen (2004), p. 38: «The shift map is without doubt the fundamental object in symbolic dynamics.»
- Sutner (1991).
- Wolfram (2002), p. 1093.
- Toffoli & Margolus (1987), section 12.8.2, «Critters», pp. 132—134; Margolus (1999); Marotta (2005).
- Toffoli & Margolus (1987), Section 14.5, «Partitioning technique», pp. 150—153; Schiff (2008), Section 4.2.1, «Partitioning Cellular Automata», pp. 115—116.
- Toffoli & Margolus (1987), Chapter 12, «The Margolus Neighborhood», pp. 119—138.
- Toffoli (1977)
- Hertling (1998)
- Morita (1995)
- Kari (2005).
Литература
- Amoroso, S. & Patt, Y. N. (1972), Decision procedures for surjectivity and injectivity of parallel maps for tessellation structures, Journal of Computer and System Sciences Т. 6: 448–464, DOI 10.1016/S0022-0000(72)80013-8.
- Béal, Marie-Pierre; Carton, Olivier; Prieur, Christophe & Sakarovitch, Jacques (2003), Squaring transducers: an efficient procedure for deciding functionality and sequentiality, Theoretical Computer Science Т. 292 (1): 45–63, DOI 10.1016/S0304-3975(01)00214-6.
- Blanchard, Paul; Devaney, Robert L. & Keen, Linda (2004), Complex dynamics and symbolic dynamics, in Williams, Susan G., Symbolic Dynamics and its Applications, vol. 60, Proceedings of Symposia in Applied Mathematics, Providence, RI: American Mathematical Society, с. 37–60, DOI 10.1090/psapm/060/2078845.
- Boykett, Tim (2004), Efficient exhaustive listings of reversible one dimensional cellular automata, Theoretical Computer Science Т. 325 (2): 215–247, DOI 10.1016/j.tcs.2004.06.007.
- Boykett, Tim; Kari, Jarkko & Taati, Siamak (2008), Conservation laws in rectangular CA, Journal of Cellular Automata Т. 3 (2): 115–122, <http://pub.math.leidenuniv.nl/~taatis/articles/conslaws06.pdf>. Проверено 1 октября 2017. Архивная копия от 30 сентября 2015 на Wayback Machine.
- Capobianco, Silvio & Toffoli, Tommaso (2011), Can anything from Noether’s theorem be salvaged for discrete dynamical systems?, Proceedings of the 10th International Conference on Unconventional Computation (UC 2011), vol. 6714, Lecture Notes in Computer Science, Springer-Verlag, с. 77–88, DOI 10.1007/978-3-642-21341-0_13.
- Chai, Zhenchuan; Cao, Zhenfu & Zhou, Yuan (2005), Encryption based on reversible second-order cellular automata, Parallel and Distributed Processing and Applications (ISPA 2005 Workshops), vol. 3759, Lecture Notes in Computer Science, Springer-Verlag, с. 350–358, DOI 10.1007/11576259_39.
- Culik, Karel, II (1987), On invertible cellular automata, Complex Systems Т. 1 (6): 1035–1044, <http://www.complex-systems.com/pdf/01-6-1.pdf>.
- Czeizler, Eugen (2004), On the size of the inverse neighborhoods for one-dimensional reversible cellular automata, Theoretical Computer Science Т. 325 (2): 273–284, DOI 10.1016/j.tcs.2004.06.009.
- Czeizler, Eugen & Kari, Jarkko (2007), A tight linear bound on the synchronization delay of bijective automata, Theoretical Computer Science Т. 380 (1–2): 23–36, DOI 10.1016/j.tcs.2007.02.052.
- Di Gregorio, S. & Trautteur, G. (1975), On reversibility in cellular automata, Journal of Computer and System Sciences Т. 11 (3): 382–391, DOI 10.1016/S0022-0000(75)80059-6.
- Durand-Lose, Jérôme (2001), Representing reversible cellular automata with reversible block cellular automata, Discrete models: combinatorics, computation, and geometry (Paris, 2001), Discrete Math. Theor. Comput. Sci. Proc., AA, Maison Inform. Math. Discrèt. (MIMD), Paris, с. 145–154.
- Durand-Lose, Jérôme (2002), Computing inside the billiard ball model, in Adamatzky, Andrew, Collision-Based Computing, Springer-Verlag, с. 135–160.
- Feynman, Richard P. (1982), Simulating physics with computers, International Journal of Theoretical Physics Т. 21 (6–7): 467–488, DOI 10.1007/BF02650179.
- Fredkin, Edward & Toffoli, Tommaso (1982), Conservative logic, International Journal of Theoretical Physics Т. 21 (3–4): 219–253, DOI 10.1007/BF01857727. Reprinted in Adamatzky, Andrew, ed. (2002), Collision-Based Computing, Springer-Verlag, с. 47–82.
- Fukś, Henryk (2007), Remarks on the critical behavior of second order additive invariants in elementary cellular automata, Fundamenta Informaticae Т. 78 (3): 329–341.
- Hattori, Tetsuya & Takesue, Shinji (1991), Additive conserved quantities in discrete-time lattice dynamical systems, Physica D: Nonlinear Phenomena Т. 49 (3): 295–322, DOI 10.1016/0167-2789(91)90150-8.
- Hedlund, G. A. (1969), Endomorphisms and automorphisms of the shift dynamical systems, Mathematical Systems Theory Т. 3 (4): 320–375, DOI 10.1007/BF01691062.
- Hertling, Peter (1998), Embedding cellular automata into reversible ones, Unconventional models of computation (Auckland, 1998), Springer Series in Discrete Mathematics and Theoretical Computer Science, Springer-Verlag, с. 243–256.
- Hillman, David (1991), The structure of reversible one-dimensional cellular automata, Physica D: Nonlinear Phenomena Т. 52 (2–3): 277–292, DOI 10.1016/0167-2789(91)90128-V.
- Janzing, Dominik (2010), Is there a physically universal cellular automaton or Hamiltonian?.
- Kari, Jarkko (1990), Reversibility of 2D cellular automata is undecidable, Physica D: Nonlinear Phenomena Т. 45 (1–3): 379–385, DOI 10.1016/0167-2789(90)90195-U.
- Kari, Jarkko (1992), On the inverse neighborhoods of reversible cellular automata, Lindenmayer Systems: Impacts on Theoretical Computer Science, Computer Graphics, and Developmental Biology, Springer-Verlag, с. 477–495.
- Kari, Jarkko (1996), Representation of reversible cellular automata with block permutations, Mathematical Systems Theory Т. 29 (1): 47–61, DOI 10.1007/BF01201813.
- Kari, Jarkko (2005), Reversible cellular automata, Developments in Language Theory: 9th International Conference, DLT 2005, Palermo, Italy, July 4–8, 2005, Proceedings, vol. 3572, Lecture Notes in Computer Science, Springer-Verlag, с. 2–23, doi:10.1007/11505877_5.
- Kari, Jarkko (2009), Structure of reversible cellular automata, Unconventional Computation: 8th International Conference, UC 2009, Ponta Delgada, Portugal, September 7–11, 2009, Proceedings, vol. 5715, Lecture Notes in Computer Science, Springer-Verlag, с. 6, DOI 10.1007/978-3-642-03745-0_5.
- Margolus, Norman (1984), Physics-like models of computation, Physica D: Nonlinear Phenomena Т. 10: 81–95, DOI 10.1016/0167-2789(84)90252-5. Reprinted in Wolfram, Stephen (1986), Theory and Applications of Cellular Automata, vol. 1, Advanced series on complex systems, World Scientific, с. 232–246, and in Adamatzky, Andrew, ed. (2002), Collision-Based Computing, Springer-Verlag, с. 83–104.
- Margolus, Norman (1999), Crystalline computation, in Hey, Anthony J. G., Feynman and Computation, Perseus Books, с. 267–305.
- Marotta, Sebastian M. (2005), Living in Critters' world, Revista Ciências Exatas e Naturais Т. 7 (1), <http://web01.unicentro.br/revistas/index.php/RECEN/article/viewFile/385/537>. Проверено 1 октября 2017. Архивная копия от 19 марта 2012 на Wayback Machine.
- McIntosh, Harold V. (2009), 12. Reversible cellular automata, One Dimensional Cellular Automata, Luniver Press, с. 205–246.
- Meyer, David A. (1996), From quantum cellular automata to quantum lattice gases, Journal of Statistical Physics Т. 85 (5–6): 551–574, DOI 10.1007/BF02199356.
- Miller, Daniel B. & Fredkin, Edward (2005), Two-state, reversible, universal cellular automata in three dimensions, Proceedings of the 2nd Conference on Computing Frontiers (CF '05), New York, NY, USA: ACM, с. 45–51, ISBN 1-59593-019-1, DOI 10.1145/1062261.1062271.
- Miller, Daniel B. & Fredkin, Edward (2012), Circular motion of strings in cellular automata, and other surprises.
- Moraal, Hendrik (2000), Graph-theoretical characterization of invertible cellular automata, Physica D: Nonlinear Phenomena Т. 141 (1–2): 1–18, DOI 10.1016/S0167-2789(00)00020-8.
- Morita, Kenichi (1995), Reversible simulation of one-dimensional irreversible cellular automata, Theoretical Computer Science Т. 148 (1): 157–163, DOI 10.1016/0304-3975(95)00038-X.
- Myhill, John (1963), The converse of Moore's Garden-of-Eden theorem, Proceedings of the American Mathematical Society Т. 14: 685–686, DOI 10.2307/2034301. Reprinted in Burks, Arthur W. (1970), Essays on Cellular Automata, University of Illinois Press, с. 204–205.
- Nagaj, Daniel & Wocjan, Pawel (2008), Hamiltonian quantum cellular automata in one dimension, Physical Review A Т. 78: 032311, DOI 10.1103/PhysRevA.78.032311.
- Patt, Y. N. (1971), Injections of neighborhood size three and four on the set of configurations from the infinite one-dimensional tessellation automata of two-state cells, Technical Report ECON-N1-P-1, Ft. Monmouth, NJ 07703. As cited by Amoroso & Patt (1972) and Toffoli & Margolus (1990).
- Pomeau, Y. (1984), Invariants in cellular automata, Journal of Physics A: Mathematical and General Т. 17 (8): L415–L418, DOI 10.1088/0305-4470/17/8/004.
- Richardson, D. (1972), Tessellations with local transformations, Journal of Computer and System Sciences Т. 6: 373–388, DOI 10.1016/S0022-0000(72)80009-6.
- Schaeffer, Luke (2015), A physically universal cellular automaton, Proceedings of the 6th Innovations in Theoretical Computer Science Conference (ITCS 2015), Association for Computing Machinery, с. 237–246, ECCC TR14-084, DOI 10.1145/2688073.2688107.
- Schiff, Joel L. (2008), Cellular Automata: A Discrete View of the World, Wiley, ISBN 978-0-470-16879-0.
- Schumacher, B. & Werner, R. F. (2004), Reversible quantum cellular automata.
- Seck Tuoh Mora, Juan Carlos; Chapa Vergara, Sergio V.; Juárez Martínez, Genaro & McIntosh, Harold V. (2005), Procedures for calculating reversible one-dimensional cellular automata, Physica D: Nonlinear Phenomena Т. 202 (1–2): 134–141, DOI 10.1016/j.physd.2005.01.018.
- Shepherd, D. J.; Franz, T. & Werner, R. F. (2006), A universally programmable quantum cellular automaton, Physical Review Letters Т. 97: 020502, PMID 16907423, DOI 10.1103/PhysRevLett.97.020502.
- Sutner, Klaus (1991), De Bruijn graphs and linear cellular automata, Complex Systems Т. 5: 19–30, <http://www.complex-systems.com/pdf/05-1-3.pdf>.
- Takesue, Shinji (1990), Relaxation properties of elementary reversible cellular automata, Physica D: Nonlinear Phenomena Т. 45 (1–3): 278–284, DOI 10.1016/0167-2789(90)90195-U.
- Toffoli, Tommaso (1977), Computation and construction universality of reversible cellular automata, Journal of Computer and System Sciences Т. 15 (2): 213–231, DOI 10.1016/S0022-0000(77)80007-X.
- Toffoli, Tommaso & Margolus, Norman (1987), Cellular Automata Machines: A New Environment for Modeling, MIT Press, ISBN 9780262200608.
- Toffoli, Tommaso & Margolus, Norman (1990), Invertible cellular automata: a review, Physica D: Nonlinear Phenomena Т. 45 (1–3): 229–253, DOI 10.1016/0167-2789(90)90185-R.
- Vichniac, Gérard Y. (1984), Simulating physics with cellular automata, Physica D: Nonlinear Phenomena Т. 10: 96–115, DOI 10.1016/0167-2789(84)90253-7.
- Watrous, John (1995), On one-dimensional quantum cellular automata, Proceedings of the 36th Annual Symposium on Foundations of Computer Science (Milwaukee, WI, 1995), Los Alamitos, CA: IEEE Computer Society Press, с. 528–537, DOI 10.1109/SFCS.1995.492583.
- Wolfram, Stephen (1984), Cellular automata as models of complexity, Nature Т. 311: 419–424, doi:10.1038/311419a0, <http://www.stephenwolfram.com/publications/academic/cellular-automata-models-complexity.pdf>.
- Wolfram, Stephen (2002), A New Kind of Science, Wolfram Media, ISBN 1-57955-008-8