Метод непосредственного применения законов Кирхгофа

Рассмотрим расчёт электрической цепи, не содержащей источников тока. Рассматриваемая цепь состоит из В ветвей и У узлов. Её расчёт сводится к нахождению токов в В ветвях. Для этого необходимо составить (У — 1) независимых уравнений по первому правилу Кирхгофа и К = (В — У + 1) независимых уравнений по второму правилу Кирхгофа. Соответствующие этим уравнениям узлы и контуры называются независимыми (то есть содержащими хотя бы одну ветвь, не принадлежащую другим узлам/контурам).

Для решения составленной системы линейных алгебраических уравнений можно воспользоваться матричной формой

${\displaystyle AI=BE}$,

где

${\displaystyle A}$ и ${\displaystyle B}$ — квадратные матрицы коэффициентов при токах и ЭДС порядка B;

${\displaystyle I}$ и ${\displaystyle E}$ — матрицы-столбцы неизвестных токов и заданных ЭДС.

Решение системы:

${\displaystyle I=A^{-1}BE=GE}$,

${\displaystyle A^{-1}}$	${\displaystyle ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1B}\\a_{21}&a_{22}&\cdots &a_{2B}\\\vdots &\vdots &\ddots &\vdots \\a_{B1}&a_{B2}&\cdots &a_{BB}\end{bmatrix}}^{-1}=}$
	${\displaystyle ={\frac {1}{\Delta }}{\begin{bmatrix}\Delta _{11}&\Delta _{12}&\cdots &\Delta _{1B}\\\Delta _{21}&\Delta _{22}&\cdots &\Delta _{2B}\\\vdots &\vdots &\ddots &\vdots \\\Delta _{B1}&\Delta _{B2}&\cdots &\Delta _{BB}\end{bmatrix}}^{T}=}$
	${\displaystyle ={\frac {1}{\Delta }}{\begin{bmatrix}\Delta _{11}&\Delta _{21}&\cdots &\Delta _{B1}\\\Delta _{12}&\Delta _{22}&\cdots &\Delta _{B2}\\\vdots &\vdots &\ddots &\vdots \\\Delta _{1B}&\Delta _{2B}&\cdots &\Delta _{BB}\end{bmatrix}}}$

— обратная матрица; ${\displaystyle \Delta }$ — определитель матрицы A; ${\displaystyle \Delta _{ik}}$ — алгебраические дополнения элементов ${\displaystyle a_{ik}}$ (см. способы нахождения обратной матрицы).

${\displaystyle G=A^{-1}B={\begin{bmatrix}g_{11}&g_{12}&\cdots &g_{1B}\\g_{21}&g_{22}&\cdots &g_{2B}\\\vdots &\vdots &\ddots &\vdots \\g_{B1}&g_{B2}&\cdots &g_{BB}\end{bmatrix}}}$

— матрица собственных ${\displaystyle g_{ii}}$ и взаимных ${\displaystyle g_{ik}}$ проводимостей (см. метод наложения).

${\displaystyle \left\{{\begin{matrix}I_{1}=g_{11}E_{1}+g_{12}E_{2}+\cdots +g_{1B}E_{B};\\I_{2}=g_{21}E_{1}+g_{22}E_{2}+\cdots +g_{2B}E_{B};\\\vdots \\I_{B}=g_{B1}E_{1}+g_{B2}E_{2}+\cdots +g_{BB}E_{B};\end{matrix}}\right.}$

— система уравнений, определяющих токи ветвей.

Зачастую при расчёте цепей подобным методом возникает необходимость составления большого количества уравнений и последующего расчёта матриц большого порядка. Поэтому на практике применяются и другие методы расчёта.

Эквивалентная схема электрической цепи

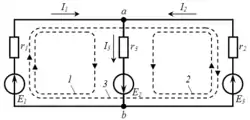
В качестве примера рассмотрим расчёт цепи, схема которой показана на рисунке — она содержит У = 2 узла и В = 3 ветви, то есть К = В − У + 1 = 3 − 2 + 1 = 2 независимых контура (на рисунке контуры отмечены пунктирной линией — можно выбрать любую пару из них — 1 и 2, или 2 и 3, или 1 и 3).

Произвольно выбираем положительные направления токов ветвей ${\displaystyle I_{1}}$, ${\displaystyle I_{2}}$, ${\displaystyle I_{3}}$ (на рисунке направления уже отмечены). По первому закону Кирхгофа можно составить одно (У − 1 = 2 − 1 = 1) независимое уравнение, например для узла a

${\displaystyle -I_{1}-I_{2}+I_{3}=0}$,

и по второму закону Кирхгофа — два (К = 2) независимых уравнения, например, для контуров 1 и 2

${\displaystyle r_{1}I_{1}+r_{3}I_{3}=E_{1}+E_{2}}$;

${\displaystyle r_{2}I_{2}+r_{3}I_{3}=E_{2}+E_{3}}$.

Представим систему из этих трёх уравнений в матричной форме:

${\displaystyle {\begin{matrix}Y-1&\left\{~\right.\\K&\left\{{\begin{matrix}~\\~\end{matrix}}\right.\end{matrix}}{\begin{bmatrix}1&1&-1\\r_{1}&0&r_{3}\\0&r_{2}&r_{3}\end{bmatrix}}{\begin{bmatrix}I_{1}\\I_{2}\\I_{3}\end{bmatrix}}=AI={\begin{bmatrix}0&0&0\\1&0&1\\0&1&1\end{bmatrix}}{\begin{bmatrix}E_{1}\\E_{2}\\E_{3}\end{bmatrix}}=BE}$

или

${\displaystyle {\begin{bmatrix}I_{1}\\I_{2}\\I_{3}\end{bmatrix}}}$	${\displaystyle ={\begin{bmatrix}1&1&-1\\r_{1}&0&r_{3}\\0&r_{2}&r_{3}\end{bmatrix}}^{-1}{\begin{bmatrix}0&0&0\\1&0&1\\0&1&1\end{bmatrix}}{\begin{bmatrix}E_{1}\\E_{2}\\E_{3}\end{bmatrix}}=}$
	${\displaystyle ={\frac {1}{-(r_{1}r_{2}+r_{1}r_{3}+r_{2}r_{3})}}{\begin{bmatrix}-r_{2}r_{3}&-r_{1}r_{3}&r_{1}r_{2}\\-(r_{2}+r_{3})&r_{3}&-r_{2}\\r_{3}&-(r_{1}+r_{3})&-r_{1}\end{bmatrix}}^{T}{\begin{bmatrix}0&0&0\\1&0&1\\0&1&1\end{bmatrix}}{\begin{bmatrix}E_{1}\\E_{2}\\E_{3}\end{bmatrix}}=}$
	${\displaystyle ={\frac {1}{r^{2}}}{\begin{bmatrix}r_{2}r_{3}&r_{2}+r_{3}&-r_{3}\\r_{1}r_{3}&-r_{3}&r_{1}+r_{3}\\-r_{1}r_{2}&r_{2}&r_{1}\end{bmatrix}}{\begin{bmatrix}0&0&0\\1&0&1\\0&1&1\end{bmatrix}}{\begin{bmatrix}E_{1}\\E_{2}\\E_{3}\end{bmatrix}}=}$
	${\displaystyle ={\frac {1}{r^{2}}}{\begin{bmatrix}r_{2}+r_{3}&-r_{3}&r_{2}\\-r_{3}&r_{1}+r_{3}&r_{1}\\r_{2}&r_{1}&r_{1}+r_{2}\end{bmatrix}}{\begin{bmatrix}E_{1}\\E_{2}\\E_{3}\end{bmatrix}}=[G][E].}$

Теперь составим систему уравнений токов:

${\displaystyle \left\{{\begin{matrix}I_{1}=g_{11}E_{1}+g_{12}E_{2}+g_{13}E_{3};\\I_{2}=g_{21}E_{1}+g_{22}E_{2}+g_{23}E_{3};\\I_{3}=g_{31}E_{1}+g_{32}E_{2}+g_{33}E_{3},\end{matrix}}\right.}$

где

${\displaystyle g_{11}=(r_{2}+r_{3})/r^{2}}$;

${\displaystyle g_{22}=(r_{1}+r_{3})/r^{2}}$;

${\displaystyle g_{33}=(r_{1}+r_{2})/r^{2}}$;

${\displaystyle g_{12}=g_{21}=-r_{3}/r^{2}}$;

${\displaystyle g_{13}=g_{31}=r_{2}/r^{2}}$;

${\displaystyle g_{23}=g_{32}=r_{1}/r^{2}}$;

${\displaystyle r={\sqrt {r_{1}r_{2}+r_{1}r_{3}+r_{2}r_{3}}}}$.

При расчёте схем замещения с источниками тока возможны упрощения, поскольку токи ветвей с источниками тока известны, и рассчитывать их не нужно. Поэтому число независимых контуров (без источников тока), для которых необходимо составить уравнения по второму закону Кирхгофа, равно К = (В — В${\displaystyle _{J}}$ — У + 1), где В${\displaystyle _{J}}$ — число ветвей с источниками тока.

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6