Метод схемных определителей
Метод схемных определителей — это символьный метод анализа электрических цепей, в котором для расчёта искомых токов и напряжений используется непосредственно схема замещения цепи с произвольными линейными элементами, минуя составление уравнений равновесия. Метод предназначен для получения оптимальных по сложности символьных выражений схемных функций, откликов, погрешностей преобразования и допусков элементов, а также параметров макромоделей подсхем и параметров неизвестных элементов в линейных электрических цепях.
Формулы выделения параметров
В основе метода схемных определителей лежат формулы Фойснера для выделения параметров двухполюсных элементов[1][2], которые могут быть представлены в схемно-алгебраической форме[3]:

В общем случае произвольный параметр может быть выделен с помощью следующего выражения:
где χ є (R, g, K, G, H, B); Δ(χ→∞) — определитель первой производной схемы, полученной из исходной схемы в результате присвоения параметру χ значения, стремящегося к бесконечности (сопротивление удаляется, проводимость заменяется на схеме идеальным проводником (стягивается), управляемые источники заменяются на нуллоры)[4]; Δ(χ=0) — определитель второй производной схемы, которая образована в результате нейтрализации выделяемого элемента, то есть принятия χ=0 (сопротивление стягивается, проводимость удаляется, управляемые источники нейтрализуется). В качестве определителей будем рассматривать символьные определители, то есть аналитические выражения, в которых все параметры схемы представлены символами, а не числами[5][6]. Нуллором называют схемную модель идеального усилителя Теллегена[7], то есть управляемый источник, параметр которого стремится к бесконечности. Нуллор является аномальным управляемым источником, поскольку ток и напряжение норатора (управляемой ветви нуллора) не определены, а ток и напряжение нуллатора (управляющей ветви нуллора) равны нулю. При замещении управляемого источника его управляемая и управляющая ветвь заменяются на норатор и нуллатор соответственно. При нейтрализации управляемая ветвь напряжения и ветвь управляющего тока стягиваются, а управляемая ветвь тока и ветвь управляющего напряжения удаляются. Идеальный проводник и разомкнутая ветвь являются частными случаями включения нуллора. Идеальный проводник эквивалентен однонаправленному параллельному соединению норатора и нуллатора, а разомкнутая ветвь — их встречному последовательному соединению. При изменении направления норатора или нуллатора знак определителя схемы, содержащей эти элементы, изменяется на противоположный. Если конденсаторы задать в операторном виде ёмкостными проводимостями рС, а индуктивности — индуктивными сопротивлениями pL, то результатом разложения символьного определителя схемы по формулам (1)-(3) становится выражение, не содержащее дробей, что делает его простым и удобным в рассмотрении. Схемные элементы по формуле (3) выделяются рекурсивно до тех пор, пока не будет получена простейшая схема, определитель которой выводится из закона Ома (например, разомкнутые сопротивление или проводимость (рис. 1,а и б), замкнутые на себя сопротивление или проводимость (рис. 1,в и г), два несоединенных узла (рис. 1,д), одиночный узел (рис. 1,е), контур с нуллором (рис. 1,ж), разомкнутая ветвь с норатором и нуллатором (рис. 1,з), контур с УИ (рис. 1,и-м)).

К описанному базису простейших схем целесообразно также добавить схемы на рис. 1,н и рис. 1,о, состоящие из двух контуров с ИНУН или ИТУТ соответственно, так как нейтрализация одного из УИ приводит к получению схемы-узла. Аналогичным свойством обладают обобщения этих схем, которые состоят из m контуров с УИ (m>2) и имеют определители Δ=K1 • K2 • … • Km+1 и Δ=B1 • B2 • … • Bm+1 соответственно.
Вырождение схем
В системном определителе (матрице) схемы возможно появление строк, которые состоят из элементов, равных нулю. Соответствующая этому определителю схема называется вырожденной. Таким образом, определитель вырожденной схемы тождественно равен нулю. С физической точки зрения принимается, что вырожденной является схема, в которой развиваются бесконечно большие токи и напряжения или значения токов и напряжений оказываются неопределёнными[8]. Так, внутренние сопротивления управляемой ветви напряжения и ветви управляющего тока равны нулю, поэтому в контуре, содержащем только управляемые ветви напряжения и ветви управляющих токов, создаётся бесконечно большой ток. С другой стороны, внутренние проводимости управляемой ветви тока и ветви управляющего напряжения равны нулю, поэтому на элементах сечения, образованного только управляемыми ветвями тока и ветвями управляющих напряжений, появляются бесконечно большие значения напряжений. Метод схемных определителей предоставляет возможность устанавливать вырожденность схемы непосредственно по её структуре и составу элементов во избежание излишних выкладок[7][8]. Ниже приведены условия вырождения схемы и нейтрализации элементов при замыкании и размыкании ветвей (табл. 1) и в контурах и сечениях (табл. 2).
| Элемент схемы | Петля | Разомкнутая ветвь |
|---|---|---|
| Сопротивление | Выделение | Нейтрализация |
| Проводимость | Нейтрализация | Выделение |
| Управляемая ветвь напряжения | Вырождение | Нейтрализация |
| Ветвь управляющего тока | Вырождение | Нейтрализация |
| Управляемая ветвь тока | Нейтрализация | Вырождение |
| Ветвь управляющего напряжения | Нейтрализация | Вырождение |
| Норатор | Вырождение | Вырождение |
| Нуллатор | Вырождение | Вырождение |
| Элемент схемы | Инцидентность элемента | |||
| контуру | сечению | |||
| из управляемой ветви напряжения или норатора | из ветви управляющего тока или нуллатора | из управляемой ветви тока или норатора | из ветви управляющего напряжения или нуллатора | |
| Сопротивление | − | Стягивание | ||
| Проводимость | Удаление | − | ||
| Управляемая ветвь напряжения | Вырождение | − | Стягивание | − |
| Ветвь управляющего тока | − | Вырождение | − | Стягивание |
| Управляемая ветвь тока | Удаление | − | Вырождение | − |
| Ветвь управляющего напряжения | − | Удаление | − | Вырождение |
| Норатор | − | Вырождение | − | Вырождение |
| Нуллатор | Вырождение | − | Вырождение | − |
Схемно-алгебраические формулы
Любая схемная функция электрической цепи может рассматриваться как отношение N/D[9]. Числитель N здесь является определителем схемы, в которой независимый источник и ветвь искомого отклика замещаются нуллором, а знаменатель D — определителем схемы с нейтрализованными входом и выходом. На рис. 2 эти правила проиллюстрированы схемно-алгебраическими формулами для шести известных схемных функций: коэффициента передачи по напряжению (рис. 2,а), передаточного сопротивления (рис. 2,б), передаточной проводимости (рис. 2,в), коэффициента передачи по току (рис. 2,г), входных проводимости (рис. 2,д) и сопротивления (рис. 2,е) соответственно[10].

При наличии в цепи нескольких независимых источников для применения аппарата схемных определителей следует использовать метод наложения[6].
Правило смены знаков в схемах с НУИ

В схемах, содержащих более одного направленного нуллора, они должны быть пронумерованы таким образом, чтобы нораторы и нуллаторы, относящиеся к одному нуллору, имели одинаковые номера:
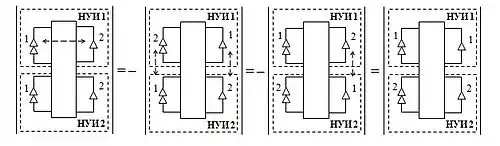
При формулировке данного правила ориентация нораторов и нуллаторов не меняется (то есть они направлены вверх).
Приложения метода схемных определителей
Метод схемных определителей используется для решения различных задач теории цепей:
См. также
- Фойснер, Фридрих Вильгельм
- Symbolic Circuit Analysis Diagnostics and Synthesis (SCADS)
Примечания
- Feussner W. Ueber Stromverzweigung in netzformigen Leitern // Annalen der Physik. — 1902. — Bd 9, N 13. — S. 1304—1329
- Feussner W. Zur Berechnung der Stromstarke in netzformigen Leitern // Annalen der Physik. — 1904. — Bd 15, N 12. — S. 385—394
- Горшков К. С., Филаретов В. В. Синтез электрических цепей на основе схемного подхода. — LAP LAMBERT Academic Publishing GmbH & Co. KG, 2011. — 242 c
- . Hashemian R. Symbolic representation of network transfer functions using norator-nullator pairs // Electronic circuits and systems.- 1977.- Vol. 1, No. 6 (November).- P. 193—197
- Филаретов В. В. Топологический анализ электронных схем методом выделения параметров // Электричество.- 1998.- № 5.- С. 43-52
- Филаретов В. В. Топологический анализ электрических цепей на основе схемного подхода: Дис. … докт. техн. наук 05.09.05 (Теоретическая электротехника) / Ульяновский гос. техн. ун-т, Санкт-Петербургский гос. техн. ун-т. — Ульяновск-Санкт-Петербург, 2002. — 265 с
- Tellegen B.D.H. On nullators and norators // IEEE Transactions on circuit theory.- 1966.- CT-13.- N 4.- P. 466—469
- Курганов С. А., Филаретов В. В. Схемно-алгебраический анализ, диакоптика и диагностика линейных электрических цепей: Учебное пособие. — Ульяновск: УлГТУ, 2005. — 320 с
- Braun J. Topological analysis of networks containing nullators and norators // Electronics letters.- 1966.- Vol. 2, No. 11.- P. 427—428
- Горшков К. С., Филаретов В. В. Обобщение метода символьного анализа Миддлбрука для расчёта допусков электрических цепей // Электроника и связь: Тематический выпуск «Электроника и нанотехнологии». — Киев, 2010.- № 5. — С. 60-64
- Filaretov V.V., Korotkov A.S. Generalized parameter extraction method in network symbolic analysis // Proceedings of the European conference on circuit theory and design (ECCTD-2003).- Kraków, Poland, 2003.- Vol. 2.- P. 406—409
- Filaretov V.V., Korotkov A.S. Generalized parameter extraction method in case of multiple excitation // Proceedings of the 8-th international workshop on Symbolic Methods and Applications in Circuit Design.-Wroclaw (September 23-24).-2004.-P. 8-11
- Коротков А. С., Курганов С. А., Филаретов В. В. Символьный анализ дискретно-аналоговых цепей с переключаемыми конденсаторами // Электричество.- 2009.-№ 4.- С. 37-46
- Филаретов В. В. Метод двоичных векторов для топологического анализа электронных схем по частям //Электричество.-2001.-№ 8.-С.33-42
- Курганов С. А. Символьный анализ и диакоптика электрических цепей: Дис. … докт. техн. наук 05.09.05 (Теоретическая электротехника) / Ульяновский гос. техн. ун-т, Санкт-Петербургский гос. техн. ун-т. — Ульяновск-Санкт-Петербург, 2006. — 328 с
- Горшков К. С. Структурный синтез и символьный допусковый анализ электрических цепей методом схемных определителей: Автореф. дис. … канд. техн. наук / МЭИ (ТУ), 2010
- Filaretov V., Gorshkov K. Transconductance Realization of Block-diagrams of Electronic Networks // Proc. of International Conference on Signals and Electronic Systems (ICSES`08). — Krakow, Poland. — 2008. — Р. 261—264
- Filaretov V., Gorshkov K., Mikheenko A. A circuit synthesis technique based on network determinant expansion // Proc. of International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD).- Seville, Spain.- Sept. 2012.- P. 293—296.
- Filaretov V., Gorshkov K. The Generalization of the Extra Element Theorem for Symbolic Circuit Tolerance Analysis // Journal of Electrical and Computer Engineering.- Vol. 2011.- Article ID 652706.- 5 p
- Филаретов В. В. Схемное отображение матрицы для символьного решения систем линейных алгебраических уравнений // Логико-алгебраические методы, модели, прикладные применения: Тр. международ. конф. КЛИН-2001.- Ульяновск: УлГТУ, 2001.-Т.3.-С.13-15