Операторный метод расчёта переходных процессов

Операторный метод — это метод расчёта переходных процессов в электрических цепях, основанный на переносе расчёта переходного процесса из области функций действительной переменной (времени t) в область функций комплексной переменной (либо операторной переменной), в которой дифференциальные уравнения преобразуются в алгебраические.

Преобразование цепи при расчёте переходных процессов операторным методом

Преобразование функций действительного переменного в операторную функцию производится с помощью методов операционного исчисления. Например, если в цепи имеется источник постоянной ЭДС ${\displaystyle E=100B}$, то в операторной схеме замещения вместо неё будет операторная ЭДС ${\displaystyle {\frac {E}{p}}={\frac {100}{p}}}$.

Последовательность расчёта операторным методом:

1. определяются независимые начальные условия;
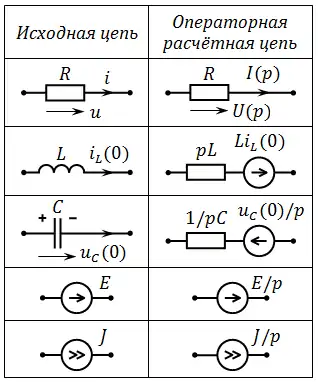
2. вычерчивается операторная схема замещения, при этом электрические сопротивления заменяются эквивалентными операторными сопротивлениями, источники тока и источники ЭДС заменяются соответствующими операторными ЭДС, при этом следует учесть, что на месте реактивных сопротивлений помимо операторных сопротивлений появляются дополнительные операторные ЭДС;
3. находятся операторные функции токов и напряжений в цепи одним из методов расчёта электрической цепи с помощью решения обыкновенных алгебраических уравнений и их систем;
4. производится преобразование найденных операторных функций токов и напряжений в функцию действительного переменного с помощью методов операционного исчисления.

Операторный метод позволяет производить расчёт сложных схем менее трудоёмко, чем классический метод.

Пример расчёта переходного процесса в электрической цепи можно посмотреть здесь.