Красный шум
Красный шум (броуновский шум) — шумовой сигнал, который производит броуновское движение. Из-за того, что по-английски он называется Brown (Brownian) noise, его название часто переводят на русский язык как коричневый шум.
 (аудио) | |
| Образец красного шума | |
| 10 секунд красного шума | |
| Помощь по воспроизведению | |
Спектр
Броуновское движение, также называемое Винеровским процессом, получается интегрированием сигнала белого шума:
это означает, что броуновское движение является интегралом белого шума , чья спектральная плотность мощности плоская:[1]
Здесь обозначает Преобразование Фурье, а - константа. Важным свойством этого преобразования является то, что производная любого распределения преобразуется как[2]
из чего можно сделать вывод, что спектр мощности броуновского шума
Индивидуальная траектория броуновского движения представляет собой спектр , где амплитуда является случайной величиной даже в пределе бесконечно длинной траектории.[3]
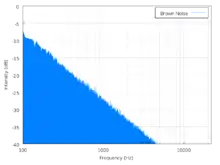
Описание
Спектральная плотность красного шума пропорциональна 1/f², где f — частота. Это означает, что на низких частотах шум имеет даже больше энергии, чем розовый шум. Энергия шума падает на 6 децибел на октаву. Акустический красный шум слышится как приглушённый, в сравнении с белым или розовым шумом.
Получение
Красный шум может быть получен путём интегрирования белого шума. То есть, тогда как (дискретный) белый шум может быть получен путём случайного выбора каждого отсчёта независимо друг от друга, красный шум может быть получен путём добавления к каждому отсчёту сигнала добавки случайной величины для получения следующего отсчёта.
См. также
Примечания
- Gardiner, C. W. Handbook of stochastic methods. — Berlin : Springer Verlag.
- Barnes, J. A.; Allan, D. W. (1966). “A statistical model of flicker noise”. Proceedings of the IEEE. 54 (2): 176—178. DOI:10.1109/proc.1966.4630. Неизвестный параметр
|name-list-style=(справка) and references therein - Krapf, Diego; Marinari, Enzo; Metzler, Ralf; Oshanin, Gleb; Xu, Xinran; Squarcini, Alessio (2018-02-09). “Power spectral density of a single Brownian trajectory: what one can and cannot learn from it”. New Journal of Physics. 20 (2): 023029. arXiv:1801.02986. Bibcode:2018NJPh...20b3029K. DOI:10.1088/1367-2630/aaa67c.