Кодекартов квадрат

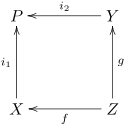
Пусть f : Z → X, g : Z → Y — морфизмы в категории C. Кодекартов квадрат для пары морфизмов (f, g) — это коммутативный квадрат следующего вида:

Более того, кодекартов квадрат является универсальным среди объектов с этим свойством. А именно, для любого объекта Q с морфизмами j₁, j₂, дополняющими f, g до коммутативного квадрата, существует единственный морфизм u : P → Q, делающий следующую диаграмму коммутативной:

Объект ${\displaystyle P=X\amalg _{Z}Y}$ с морфизмами i₁, i₂ называется расслоенным копроизведением (расслоенной суммой, амальгамой, амальгамированной суммой, англ. pushout).

Как и любые универсальные конструкции, кодекартов квадрат не обязательно существует, но если существует, то определён с точностью до изоморфизма.

• В категории множеств ${\displaystyle X\amalg _{Z}Y}$ — это дизъюнктное объединение X и Y, в котором отождествлены элементы с общим прообразом в Z. Более точно, ${\displaystyle X\amalg _{Z}Y=X\amalg Y{\big /}\sim ,}$ где ~ — наименьшее отношение эквивалентности, такое что i₁ ∘ f (z) ~ i₂ ∘ g(z).

• Конструкция склеивания пространств является примером построения расслоенных копроизведений в категории топологических пространств. Более подробно, если Z — подпространство Y и g : Z → Y — соответствующее отображение включения, то можно «склеить» Y с X по Z, используя «отображение соответствия» f : Z → X. Получившееся в результате склеенное пространство ${\displaystyle X\cup _{f}Y}$ является расслоенным копроизведением X и Y.

• В категории абелевых групп о кодекартовом квадрате можно говорить как о прямой сумме абелевых групп «со склейкой». А именно, если f и g — гомоморфизмы с общим источником Z, кодекартов квадрат является факторгруппой прямой суммы по подгруппе, порождённой всеми элементами вида (f(z), −g(z)). Примерно то же самое можно проделать в категории модулей.

• Голдблатт Р. Топосы. Категорный анализ логики = Topoi. The categorial analysis of logic / Пер. с англ. В. Н. Гришина и В. В. Шокурова под ред. Д. А. Бочвара. — М.: Мир, 1983. — 488 с.
• Маклейн С. Глава 3. Универсальные конструкции и пределы // Категории для работающего математика = Categories for the working mathematician / Пер. с англ. под ред. В. А. Артамонова. — М.: Физматлит, 2004. — С. 68—94. — 352 с. — ISBN 5-9221-0400-4.