Деление на ноль
Деление на ноль в математике — деление, при котором делитель равен нулю. Такое деление может быть формально записано как , где — делимое.
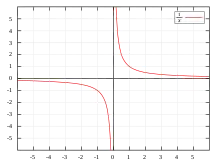
В арифметике
В обычной арифметике (с вещественными числами) данное выражение не имеет смысла, так как:
- при а ≠ 0 не существует числа, которое при умножении на 0 даёт а, поэтому ни одно число не может быть принято за частное а⁄0;
- при а = 0 деление на ноль также не определено, поскольку любое число при умножении на 0 даёт 0 и может быть принято за частное 0⁄0.
Исторически одна из первых ссылок на математическую невозможность присвоения значения а⁄0 содержится в критике Джорджа Беркли исчисления бесконечно малых.
В алгебре
Деление на ноль недопустимо во многих алгебраических структурах (например, в полях, кольцах). Однако понятие кольца можно расширить так, чтобы деление на ноль было бы возможным. Получившаяся структура называется колесо.
Логические ошибки
Поскольку при умножении любого числа на ноль в результате мы всегда получаем ноль, при делении обеих частей выражения x × 0 = y × 0, верного вне зависимости от значения x и y, на 0 получаем неверное в случае произвольно заданных переменных выражение x = y. Поскольку ноль может быть задан не явно, но в виде достаточно сложного математического выражения, к примеру в форме разности двух значений, сводимых друг к другу путём алгебраических преобразований, такое деление может быть достаточно неочевидной ошибкой. Незаметное внесение такого деления в процесс доказательства с целью показать идентичность заведомо разных величин, тем самым доказывая любое абсурдное утверждение, является одной из разновидностей математического софизма[1].
В информатике
В программировании, в зависимости от языка программирования, типа данных и значения делимого, попытка деления на ноль может приводить к различным последствиям. Принципиально различны последствия деления на ноль в целой и вещественной арифметике:
- Попытка целочисленного деления на ноль всегда является критической ошибкой, делающей невозможным дальнейшее исполнение программы. Она приводит либо к генерации исключения (которое программа может обработать сама, избежав тем самым аварийной остановки), либо к немедленной остановке программы с выдачей сообщения о неисправимой ошибке и, возможно, содержимого стека вызовов. В некоторых языках программирования, например, в Go, целочисленное деление на нулевую константу считается синтаксической ошибкой и приводит к аварийному прекращению компиляции программы.
- В вещественной арифметике последствия могут быть различным в разных языках:
- генерация исключения или остановка программы, как и при целочисленном делении;
- получение в результате операции специального нечислового значения. Вычисления при этом не прерываются, а их результат впоследствии может быть интерпретирован самой программой или пользователем как осмысленное значение или как свидетельство некорректности вычислений. Широко используется принцип, согласно которому при делении вида a⁄0, где a ≠ 0 — число с плавающей запятой, результат оказывается равен положительной или отрицательной (в зависимости от знака делимого) бесконечности —
+INFили−INF, а при a = 0 в результате получается специальное значение NaN (сокр. от англ. not a number — «не число»). Такой подход принят в стандарте IEEE 754, который поддерживается многими современными языками программирования.
Случайное деление на ноль в компьютерной программе порой становится причиной дорогих или опасных сбоев в работе управляемого программой оборудования. К примеру, 21 сентября 1997 года в результате деления на ноль в компьютеризированной управляющей системе крейсера USS Yorktown (CG-48) Военно-морского флота США произошло отключение всего электронного оборудования в системе, в результате чего силовая установка корабля прекратила свою работу[2][3].
См. также
Примечания
- Чарльз Сейфе. Устрашающие свойства пустоты // Ноль. Биография опасной идеи = Zero: The Biography of a Dangerous Idea. — Neoclassic, АСТ, 2014. — 2000 экз. — ISBN 978-5-17-083294-1, 978-985-18-3018-9.
- Sunk by Windows NT // Wired News. 1998-07-24.
- William Kahan. Desperately Needed Remedies for the Undebuggability of Large Floating-Point Computations in Science and Engineering (PDF) 54/90 (April 24, 2012 6:41 AM).
