Граф призмы

Индивидуальные графы можно назвать согласно ассоциированным телам:

• Граф треугольной призмы — 6 вершин, 9 рёбер
• Кубический граф — 8 вершин, 12 рёбер
• Граф пятиугольной призмы — 10 вершин, 15 рёбер
• Граф шестиугольной призмы — 12 вершин, 18 рёбер
• Граф семиугольной призмы — 14 вершин, 21 рёбер
• Граф восьмиугольной призмы — 16 вершин, 24 рёбер
• …

Y3 = GP(3,1)

Y4 = Q3 = GP(4,1)

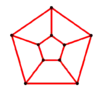Y5 = GP(5,1)

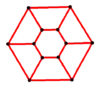Y6 = GP(6,1)

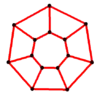Y7 = GP(7,1)

Y8 = GP(8,1)

Хотя геометрически звёздчатые многоугольники также служат гранями другой последовательности (самопересекающихся и невыпуклых) призматических многогранников, графы этих звёздчатых призм изоморфны графам призм и не образуют отдельной последовательности графов.

Графы призм являются примерами обобщённых графов Петерсена с параметрами GP(n,1). Графы также можно образовать как прямое произведение цикла и единичного ребра[1].

Как и многие вершинно-транзитивные графы, призматические графы можно построить как графы Кэли. Диэдральная группа порядка n является группой симметрий правильного n-угольника на плоскости. Она действует на n-угольник вращениями и отражениями. Группа может быть сгенерирована двумя элементами, вращением на угол ${\displaystyle 2\pi /n}$ и одним отражением, и граф Кэли этой группы с этим генерирующим множеством является графом призмы. Абстрактно группа имеет задание ${\displaystyle \langle r,f\mid r^{n},f^{2},(rf)^{2}\rangle }$ (где r — это вращение, а f — отражение) и граф Кэли имеет r и f (или r, r⁻¹ и f) в качестве генераторов [1]

Граф n-угольной призмы с нечётным n можно построить как циркулянтный граф ${\displaystyle C_{2n}^{2,n}}$, однако это построение не работает для чётных значений n [1].

Граф n-угольной призмы имеет 2n вершин и 3n рёбер. Графы являются регулярными кубическими графами. Поскольку призма имеет симметрии, переводящие любую вершину в любую другую, графы призм являются вершинно-транзитивными графами. Являясь полиэдральными графами, эти графы также являются вершинно 3-связными планарными графами. Любой граф призмы имеет гамильтонов цикл[2].

Среди всех двусвязных кубических графов графы призм имеют с точностью до постоянного множителя наибольшее возможное число 1-разложений графа. 1-разложение — это разбиение множества рёбер графа на три совершенных паросочетания, или, эквивалентно, рёберная раскраска графа тремя цветами. Любой двусвязный кубический граф с n вершинами имеет O(2^n/2) 1-разложений, а граф призмы имеет Ω(2^n/2) 1-разложений [3].

Число остовных деревьев графа n-угольной призмы задаётся формулой [4].

${\displaystyle {\frac {n}{2}}{\bigl (}(2+{\sqrt {3}})^{n}+(2-{\sqrt {3}})^{n}){\bigr .}}$

Для n = 3, 4, 5, ... эти числа равны

78, 388, 1810, 8106, 35294, ...

Графы n-угольных призм для чётных n являются частичными кубами. Они образуют одно из немногих известных бесконечных семейств кубических графов частичных кубов, и они являются (за исключением четырёх случаев) единственными вершинно-транзитивными кубическими частичными кубами[5].

Граф пятиугольной призмы является одним из запрещённых миноров для графов с древесной шириной три[6]. Графы треугольной призмы и куба имеют древесную ширину в точности три, но все бо́льшие призмы имеют древесную ширину четыре.

Другие бесконечные семейства полиэдральных графов, основанные подобным же образом из многогранников с правильными основаниями, включают графы антипризм и колёса (графы пирамид). Другими вершинно-транзитивными полиэдральными графами являются архимедовы графы.

Если два цикла призматического графа разорвать удалением одного ребра в одном и том же месте в обоих циклах, получим лестницу. Если два удалённых ребра заменить двумя скрещивающимися рёбрами, получим непланарный граф «Лестница Мёбиуса»[7].

• David Eppstein. The complexity of bendless three-dimensional orthogonal graph drawing // Journal of Graph Algorithms and Applications. — 2013. — Т. 17, вып. 1. — С. 35–55. — doi:10.7155/jgaa.00283.
• A. A. Jagers. A note on the number of spanning trees in a prism graph // International Journal of Computer Mathematics. — 1988. — Т. 24, вып. 2. — С. 151–154. — doi:10.1080/00207168808803639.
• Tilen Marc. Classification of vertex-transitive cubic partial cubes. — 2015. — arXiv:1509.04565.
• Stefan Arnborg, Andrzej Proskurowski, Derek G. Corneil. Forbidden minors characterization of partial 3-trees // Discrete Mathematics. — 1990. — Т. 80, вып. 1. — С. 1–19. — doi:10.1016/0012-365X(90)90292-P.
• Richard K. Guy, Frank Harary. On the Möbius ladders // Canadian Mathematical Bulletin. — 1967. — Т. 10. — С. 493–496. — doi:10.4153/CMB-1967-046-4.
• R. C. Read, R. J. Wilson. Chapter 6 special graphs // An Atlas of Graphs. — Oxford, England: Oxford University Press, 2004. — С. 261, 270.