Граф Дюрера

Многогранник Дюрера комбинаторно эквивалентен кубу с двумя усечёнными противоположными вершинами[1], хотя на рисунке Дюрера он, скорее, нарисован как усечённый ромбоэдр или трёхгранный усечённый трапецоид[2]. Точные геометрические свойства нарисованного Дюрером многогранника служат предметом академических споров, в которых предполагаются различные гипотетические значения (острых) углов от 72° до 82°[3].

Граф Дюрера
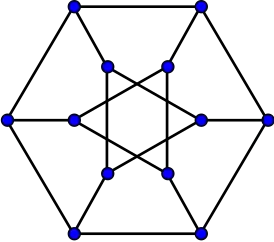Назван в честь	Альбрехт Дюрер
Вершин	12
Рёбер	18
Радиус	3
Диаметр	4
Обхват	3
Автоморфизмы	12 (D6)
Хроматическое число	3
Хроматический индекс	3
Свойства	Кубический Планарный Хорошо укрытый
Медиафайлы на Викискладе

Граф Дюрера является графом, образованным вершинами и рёбрами многогранника Дюрера. Граф является кубическим с обхватом 3 и диаметром 4. Поскольку граф является скелетом многогранника Дюрера, он может быть получен путём применения преобразования треугольник-звезда противоположных вершин графа куба или как обобщённый граф Петерсена ${\displaystyle G(6,2)}$. Как и любой другой граф выпуклого многогранника, граф Дюрера является вершинно 3-связным простым планарным графом.

Граф Дюрера является хорошо укрытым, что означает, что все его наибольшие независимые множества имеют одно и то же число вершин — четыре. Граф является одним из хорошо укрытых кубических многогранных графов и одним из семи хорошо укрытых 3-связных кубических графов. Другими тремя хорошо укрытыми простыми выпуклыми многогранниками являются тетраэдр, треугольная призма и пятиугольная призма[4][5].

Граф Дюрера является гамильтоновым с LCF-обозначением [-4,5,2,-4,-2,5;-][6]. Точнее, граф имеет ровно шесть гамильтоновых циклов, каждая пара которых может быть отображена в любую другую симметриями графа[7].

Группа автоморфизмов как графа Дюрера, так и многогранника Дюрера (в виде усечённого куба или в форме, представленной Дюрером) изоморфна диэдрической группе ${\displaystyle D_{6}}$ порядка 12.

• 
  Хроматический индекс графа Дюрера равен 3.
• 
  Хроматическое число графа Дюрера равно 3.
• 
  Граф Дюрера гамильтонов.

• S. R. Campbell, M. N. Ellingham, Gordon F. Royle. A characterisation of well-covered cubic graphs // Journal of Combinatorial Mathematics and Combinatorial Computing. — 1993. — Т. 13. — С. 193–212.
• Stephen R. Campbell, Michael D. Plummer. On well-covered 3-polytopes // Ars Combinatoria. — 1988. — Т. 25, вып. A. — С. 215–242.
• Frank Castagna, Geert Prins. Every Generalized Petersen Graph has a Tait Coloring // Pacific Journal of Mathematics. — 1972. — Т. 40. — doi:10.2140/pjm.1972.40.53.
• Allen J. Schwenk. Enumeration of Hamiltonian cycles in certain generalized Petersen graphs // Journal of Combinatorial Theory. — 1989. — Т. 47, вып. 1. — С. 53–59. — doi:10.1016/0095-8956(89)90064-6.
• P. Weber. Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus. — Strassburg, 1900. (как процитировано у Вайцеля (Вайцель (2004)).
• Hans Weitzel. A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I // Historia Mathematica. — 2004. — Т. 31, вып. 1. — С. 11–14. — doi:10.1016/S0315-0860(03)00029-6.