Гипотеза Борсука

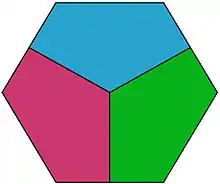
Случай ${\displaystyle n=1}$ очевиден. Случай ${\displaystyle n=2}$ был доказан самим Борсуком в 1933 году, он воспользовался результатом Дьюлы Пала (венг. Pál Gyula) 1929 года, согласно которому любую фигуру диаметра 1 можно поместить в правильный шестиугольник ширины 1, а такой шестиугольник в свою очередь допускает разрезание на три пятиугольника диаметра ${\displaystyle {\tfrac {\sqrt {3}}{2}}<1}$. Кроме того, Борсук доказал, что ${\displaystyle n}$-мерный шар нельзя разделить на ${\displaystyle n}$ частей меньшего диаметра, тем самым утвердив нижнюю оценку для количества частей (доказательство основано на теореме Борсука — Улама).

В 1946 году Хадвигер доказал справедливость гипотезы при всех ${\displaystyle n}$ для выпуклых тел с гладкой границей[2].

В 1947 году Юлиан Перкаль (польск. Julian Perkal) доказал случай ${\displaystyle n=3}$ для всех ограниченных тел[3], независимо от него в 1955 году этот же результат получил британский математик Эгглстон; простое доказательство, сходное с доказательством Борсука, было найдено несколько позже Бранко Грюнбаумом и Альдаром Хеппешем; они доказывают, что любое тело диаметра 1 можно поместить в определённый октаэдр с отсечёнными тремя вершинами, который в свою очередь допускает разбиение на 4 части диаметра меньше 0,9888.

По меньшей мере с начала 1970-х годов гипотеза подтверждена для центрально-симметричных тел. В 1971 году Клод Роджерс доказал гипотезу для всякого множества, инвариантного относительно действия группы преобразований, оставляющих на месте правильный ${\displaystyle n}$-мерный симплекс.

В 1993 году Борис Декстер установил справедливость гипотезы для выпуклых тел с поясом из регулярных точек[4], в 1995 году им же положительно решена проблема для всех тел вращения в произвольных размерностях[5].

Число Борсука ${\displaystyle f(n)}$ — наименьшее число возможных частей меньшего диаметра, на которые можно разбить всякое ограниченное тело в ${\displaystyle n}$-мерном пространстве. Параллельно с подтверждением гипотезы ${\displaystyle f(n)=n+1}$ в частных случаях, улучшались нижние и верхние оценки для ${\displaystyle f(n)}$. Сравнительно легко получены оценки ${\displaystyle f(n)\leqslant (2{\sqrt {n}}+1)^{n}}$ и ${\displaystyle f(n)\leqslant 2^{n}}$. В 1983 году Маршалл Лассак установил, что ${\displaystyle f(n)\leqslant 2^{n-1}+1}$.

Среди асимптотических верхних оценок долгое время лучшей была оценка Клода Роджерса (англ. Claude Ambrose Rogers; 1965): ${\displaystyle f(n)\leqslant {\big (}{\sqrt {2}}+o(1){\big )}^{n}}$; в 1988 году Одед Шрамм установил, что:

${\displaystyle f(n)\leqslant {\Big (}{\sqrt {\tfrac {3}{2}}}+o(1){\Big )}^{n}}$.

Отрицательное решение проблемы в общем случае выявлено в 1993 году Гилем Калаем (англ. Gil Kalai) и Джеффом Каном (англ. Jeff Kahn)[6], построившими контрпример в размерности ${\displaystyle n=1325}$, и доказавшими невыполнение гипотезы для всех ${\displaystyle n>2014}$. Кроме того, они показали, что для достаточно больших ${\displaystyle n}$, существуют ${\displaystyle n}$-мерные тела, которые нельзя разбить на ${\displaystyle {\big (}1{,}203+o(1){\big )}^{\sqrt {n}}}$ частей меньшего диаметра. В последующие годы размерность, выше которой гипотеза не выполняется, последовательно снижалась:

• 1993 — ${\displaystyle n\geqslant 2015}$ (Калай — Кан),
• 1994 — ${\displaystyle n\geqslant 946}$ (Нилли),
• 1997 — ${\displaystyle n\geqslant 903}$ (Вайссбах — Грей),
• 1997 — ${\displaystyle n\geqslant 561}$ (Райгородский)[7],
• 2000 — ${\displaystyle n\geqslant 560}$ (Вайссбах),
• 2001 — ${\displaystyle n\geqslant 324}$ (Хинрихс),
• 2002 — ${\displaystyle n\geqslant 323}$ (Пихурко),
• 2003 — ${\displaystyle n\geqslant 298}$ (Хинрихс — Рихтер)[8],
• 2013 — ${\displaystyle n\geqslant 65}$ (Бондаренко)[9],
• 2013 — ${\displaystyle n\geqslant 64}$ (Йенрих)[10].

Для построения контпримеров во всех случаях использовались конечные множества и использованы тонкие комбинаторные результаты[11]. Нижние оценки для минимального числа частей меньшего диаметра в большинстве контрпримеров — ${\displaystyle {\big (}1{,}203+o(1){\big )}^{\sqrt {n}}}$, в одном из результатов Райгородского (1999) эта оценка улучшена до ${\displaystyle {\big (}1{,}2255+o(1){\big )}^{\sqrt {n}}}$.

В 1953 году Дэвид Гейл выдвинул гипотезу, что любое тело единичного диаметра в трёхмерном пространстве допускает разбиение на 4 части с диаметром:

${\displaystyle {\sqrt {\frac {3+{\sqrt {3}}}{6}}}\approx 0{,}888}$,

то есть шар является «наихудшим» в этом смысле телом[12].

В 1971 году гипотеза Борсука подтверждена для сферического и гиперболического пространств при ${\displaystyle n=2,3}$[13].

В 1991 году этот результат обобщён на произвольные размерности для центрально-симметрических выпуклых гиперповерхностей[14].

В 2012 году изучены аналоги проблемы Борсука в пространстве ${\displaystyle \mathbb {Q} ^{n}}$ с евклидовой метрикой и с метрикой ${\displaystyle l_{p}}$[15].

В 2019 году рассмотрен вопрос о разбиении произвольных ограниченных метрических пространств на заданное количество подмножеств меньшего диаметра, и выявлены критерии осуществимости и неосуществимости такого разбиения в зависимости от расстояния по метрике Громова — Хаусдорфа от заданного пространства до симплексов заданной мощности, где под симплексом понимается метрическое пространство, в котором все ненулевые расстояния одинаковы[16].

• В. Г. Болтянский, И. Ц. Гохберг. Теоремы и задачи комбинаторной геометрии. — М.: Наука, 1965. — 108 с. — (Математическая библиотечка). (содержит доказательство гипотезы в размерностях 2 и 3)
• В. Г. Болтянский, И. Ц. Гохберг. Разбиение фигур на меньшие части/ серия = Популярные лекции по математике, выпуск 50. — М.: Наука, 1971. — 88 с.
• Б. Грюнбаум. Этюды по комбинаторной геометрии и теории выпуклых тел. — М.: Наука, 1971.
• А. М. Райгородский. Проблема Борсука. — М.: МЦНМО, 2006. — 56 с.
• А. Б. Скопенков. ${\displaystyle n}$-мерный куб, многочлены и решение проблемы Борсука // Математическое просвещение. — М.: МЦНМО, 1999. — Вып. 3 (3).