Вариация поворота кривой

Вариация поворота кривой — интеграл кривизны кривой по её длине.

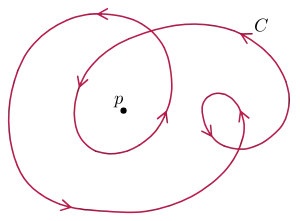
Кривая с вариацией поворота

6\cdot \pi

Определение

Вариация поворота кривой $\gamma$ на плоскости или в пространстве определяется как точная верхняя грань суммы внешних углов вписанной в $\gamma$ ломаной.

В случае если кривая $\gamma$ замкнута, вписанная ломаная также предполагается замкнутой.

Замечания

Если $\gamma \colon [a;\,b]\to \mathbb {E} ^{d}$ гладкая кривая, параметризованная длиной, $\kappa (s)$ — её кривизна, то вариация поворота равна интегралу модуля кривизны:
$\int \limits _{a}^{b}|\kappa (s)|\cdot ds.$

Вариация поворота гладкой регулярной кривой $\gamma \colon [a;\,b]\to \mathbb {E} ^{d}$ можно также определить как длину её касательной индикатрисы; то есть кривой $\tau (s)\colon [a;\,b]\to \mathbb {S} ^{d-1}$ образованной единичными касательными векторами $\tau (s)={\tfrac {{\dot {\gamma }}(s)}{|{\dot {\gamma }}(s)|}}$ .

Свойства

Теорема Фенхеля о повороте кривой: Вариация поворота любой замкнутой кривой не менее $2\pi$ . Более того, в случае равенства кривая является плоской и выпуклой.
Теорема Фари — Милнора о повороте узла: Вариация поворота любого узла больше $4\pi$ .
Неравенство ДНК. Если замкнутая плоская кривая лежит в выпуклой фигуре с периметром $2{\cdot }\pi$ то её длина не превосходит её вариацию поворота.[1]
Теорема Усова о геодезической: Вариация поворота геодезической на графике выпуклой функции $f\colon \mathbb {R} ^{2}\to \mathbb {R}$ не превосходит её удвоенной константы Липшица.[2]
Вариация поворота кратчайшей на замкнутой выпуклой поверхности ограничена универсальной константой.[3]

Вариации и обобщения

Для плоских кривых, у кривизны можно определить знак и определить поворот кривой как интеграл кривизны с знаком. Теорема о повороте кривой является дифференциальногеометрическим аналогом теоремы о сумме углов многоугольника.

Примечания

Назаров, Александр Ильич, Федор Владимирович Петров. О гипотезе С. Л. Табачникова (рус.) // Алгебра и анализ. — 2007. — Т. 19, № 1. — С. 177—193..
В. В. Усов. "О длине сферического изображения геодезической на выпуклой поверхности." Сибирский математический журнал 17.1 (1976), с. 233—236
N. Lebedeva, A. Petrunin. On the total curvature of minimizing geodesics on convex surfaces (рус.) // Алгебра и анализ. — 2017. — Т. 29, № 1. — С. 189—208.

Литература

Топоногов, В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 978-5-89155-213-5.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Назаров, Александр Ильич, Федор Владимирович Петров. О гипотезе С. Л. Табачникова (рус.) // Алгебра и анализ. — 2007. — Т. 19, № 1. — С. 177—193..

[2] В. В. Усов. "О длине сферического изображения геодезической на выпуклой поверхности." Сибирский математический журнал 17.1 (1976), с. 233—236

[3] N. Lebedeva, A. Petrunin. On the total curvature of minimizing geodesics on convex surfaces (рус.) // Алгебра и анализ. — 2017. — Т. 29, № 1. — С. 189—208.