Бикубическая интерполяция
Бикуби́ческая интерполя́ция — в вычислительной математике расширение кубической интерполяции на случай функции двух переменных, значения которой заданы на двумерной регулярной сетке. Поверхность, полученная в результате бикубической интерполяции, является гладкой функцией на границах соседних квадратов, в отличие от поверхностей, полученных в результате билинейной интерполяции или интерполяции методом ближайшего соседа.
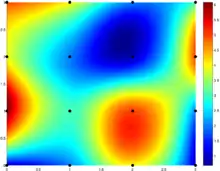
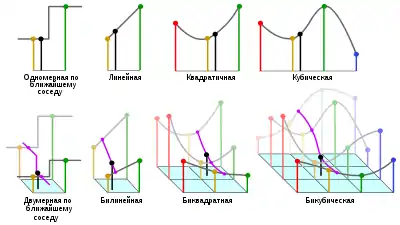
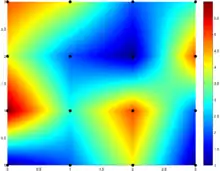
Бикубическая интерполяция часто используется в обработке изображений, давая более качественную картинку по сравнению с билинейной интерполяцией. Также бикубическая интерполяция применяется в алгоритмах управления станков с ЧПУ для учёта неровностей плоскостей, например, при фрезеровке печатных плат.
Принцип метода
В случае бикубической интерполяции значение функции в искомой точке вычисляется через её значения в 16 соседних точках, расположенных в вершинах квадратов плоскости .
При использовании приведённых ниже формул для программной реализации бикубической интерполяции следует помнить, что значения и являются относительными, а не абсолютными. Например, для точки с координатами . Для получения относительных значений координат необходимо округлить вещественные координаты вниз и вычесть полученные числа из вещественных координат.
,
где
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
Подобным образом можно использовать и интерполяции более высокого порядка, вычисляя значения функции по соседним точкам.

Бикубическая интерполяция сплайнами
Допустим, что необходимо интерполировать значение функции в точке , лежащей внутри квадрата , и известно значение функции в шестнадцати соседних точках .
Тогда общий вид функции, задающей интерполированную поверхность, может быть записан следующим образом:
.
Для нахождения коэффициентов необходимо подставить в вышеприведённое уравнение значения функции в известных шестнадцати точках. Например:
.
Полностью в матричном виде:
,
где
,
,
.
Решая получившуюся систему линейных алгебраических уравнений, можно найти значения в явном виде:
.
Единожды найденные коэффициенты теперь могут быть использованы для многократного вычисления интерполированного значения функции в произвольных точках квадрата .
Следует отметить, что такой способ обеспечивает непрерывность самой функции и её второй производной на границах смежных квадратов, но приводит к разрыву первых производных на границах ячеек 4×4. Для обеспечения непрерывности самой функции и её первой производной необходимо подставлять в исходное выражение значения функции и значения первых производных по направлениям x и y в вершинах центральной ячейки, производные рассчитываются через центральные разности. Для подстановки производных выражение должно быть продифференцировано соответствующим образом.
Последовательная кубическая интерполяция
Другая интерпретация метода заключается в том, что для нахождения интерполированного значения можно сначала произвести кубическую интерполяцию в одном направлении, а затем в другом.
Для функции с известными значениями , , , можно построить кубический сплайн: , или в матричном виде:
,
где
,
.
Таким образом, для нахождения интерполированного значения в квадрате можно сначала рассчитать четыре значения , , , для зафиксированного , затем через полученные четыре точки построить кубический сплайн, и этим завершить вычисление :
.
Следует отметить, что такой подход обеспечивает непрерывность самой функции и её вторых производных на границе ячеек, но не обеспечивает непрерывности первой производной. Для обеспечения непрерывности первой производной необходимо подставлять значения функции и её первых производных на границе центральной ячейки. Тогда коэффициенты сплайна будут иметь вид:
,
.
Литература
- R. Keys. Cubic convolution interpolation for digital image processing (англ.) // IEEE Transactions on Acoustics, Speech, and Signal Processing : journal. — 1981. — Vol. 29, no. 6. — P. 1153—1160. — doi:10.1109/TASSP.1981.1163711.
