Атмосферное давление
Атмосфе́рное давле́ние — давление атмосферы, действующее на все находящиеся в ней предметы и на земную поверхность, равное модулю силы, действующей в атмосфере, на единицу площади поверхности по нормали к ней[1]. В покоящейся стационарной атмосфере давление равно отношению веса вышележащего столба воздуха к площади его поперечного сечения. Атмосферное давление является одним из термодинамических параметров состояния атмосферы, оно изменяется в зависимости от места и времени[2]. Давление — величина скалярная, имеющая размерность L−1MT−2, измеряется барометром.
| Атмосферное давление | |
|---|---|
| Размерность | L−1MT−2 |
| Единицы измерения | |
| СИ | Па |
| СГС | дин·см-2 |
| Примечания | |
| скаляр | |
Единицей измерения в Международной системе единиц (СИ) является паскаль (русское обозначение: Па; международное: Pa). Кроме того, в Российской Федерации в качестве внесистемных единиц давления допущены к использованию бар, миллиметр ртутного столба, миллиметр водяного столба, метр водяного столба, килограмм-сила на квадратный сантиметр и атмосфера техническая[3]. Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 °C, называется нормальным атмосферным давлением (101 325 Па)[2].
История

Традиционно считалось, что всасывающие насосы работают из-за того, что «природа боится пустоты». Но голландец Исаак Бекман в тезисах своей докторской диссертации, защищенной им в 1618 году, утверждал: «Вода, поднимаемая всасыванием, не притягивается силою пустоты, но гонима в пустое место налегающим воздухом» (Aqua suctu sublata non attrahitur vi vacui, sed ab aere incumbentein locum vacuum impellitur).
В 1630 году генуэзский физик Балиани написал письмо Галилею о неудачной попытке устроить сифон для подъема воды на холм высотою примерно 21 метр. В другом письме Галилею (от 24 октября 1630 года) Балиани предположил, что подъем воды в трубе обусловлен давлением воздуха.
Наличие атмосферного давления привело людей в замешательство в 1638 году, когда не удалась затея герцога Тосканского украсить сады Флоренции фонтанами — вода не поднималась выше 10,3 метров. Поиски причин этого и опыты с более тяжёлым веществом — ртутью, предпринятые Эванджелистой Торричелли, привели к тому, что в 1643 году он доказал, что воздух имеет вес[5]. Совместно с В. Вивиани, Торричелли провёл первый опыт по измерению атмосферного давления, изобретя первый ртутный барометр — стеклянную трубку, в которой нет воздуха. В такой трубке ртуть поднимается на высоту около 760 мм.
Изменчивость и влияние на погоду
На земной поверхности атмосферное давление изменяется время от времени и от места к месту. Особенно важны определяющие погоду непериодические изменения атмосферного давления, связанные с возникновением, развитием и разрушением медленно движущихся областей высокого давления (антициклонов) и относительно быстро перемещающихся огромных вихрей (циклонов), в которых господствует пониженное давление. Отмечены колебания атмосферного давления на уровне моря в пределах 641 — 816 мм рт. ст.[6] (в центральной части смерча давление падает и может достигать значения 560 мм ртутного столба)[7].
На картах атмосферное давление изображается с помощью изобар — изолиний, соединяющих точки с одинаковым приземным атмосферным давлением, обязательно приведенным к уровню моря[8].
Атмосферное давление — очень изменчивый метеоэлемент. Из его определения следует, что оно зависит от высоты соответствующего столба воздуха, его плотности, от ускорения силы тяжести, которая меняется от широты места и высоты над уровнем моря.
1 Па = 0,0075 мм рт. ст., или 1 мм рт. ст. = 133,3 Па
Стандартное давление
В химии стандартным атмосферным давлением с 1983 года по рекомендации IUPAC считается давление, равное 100 кПа[9]. Атмосферное давление является одной из наиболее существенных характеристик состояния атмосферы. В покоящейся атмосфере давление в любой точке равно весу вышестоящего столба воздуха с единичным сечением.
В системе СГС 760 мм рт. ст. эквивалентно 1,01325 бар (1013,25 мбар) или 101 325 Па в Международной системе единиц (СИ).
Барическая ступень
Высота, на которую надо подняться или опуститься, чтобы давление изменилось на 1 гПа (гектопаскаль), называется «барической (барометрической) ступенью». Барической ступенью удобно пользоваться при решении задач, не требующих высокой точности, например, для оценки давления по известной разности высот. Считая, что атмосфера не испытывает существенного вертикального ускорения (то есть находится в квазистатическом состоянии), из основного закона статики получаем, что барическая ступень равна:
При температуре воздуха 0 °C и давлении 1000 гПа, барическая ступень равна 8 м/гПа. Следовательно, чтобы давление уменьшилось на 1 гПа, нужно подняться на 8 метров.
С ростом температуры и увеличением высоты над уровнем моря она возрастает (в частности, на 0,4 % на каждый градус нагревания), то есть она прямо пропорциональна температуре и обратно пропорциональна давлению. Величина, обратная барической ступени, — вертикальный барический градиент, то есть изменение давления при поднятии или опускании на 100 метров. При температуре 0 °C и давлении 1000 гПа он равен 12,5 гПа.
Изменения давления с высотой
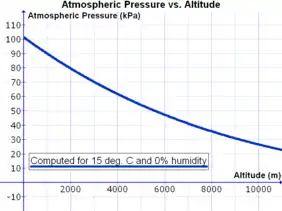
С высотой атмосферное давление уменьшается. Например, горная болезнь начинается на высоте около 2-3 км, а атмосферное давление на вершине Эвереста составляет примерно 1/4 от показателя на уровне моря.
В стационарных условиях атмосферное давление уменьшается по мере увеличения высоты, поскольку оно создаётся лишь вышележащим слоем атмосферы. Зависимость давления от высоты описывается барометрической формулой[10].
Уравнение статики выражает закон изменения давления с высотой:
где: — давление, — ускорение свободного падения, — плотность воздуха, — толщина слоя. Из основного уравнения статики следует, что при увеличении высоты () изменение давления отрицательное, то есть давление уменьшается. Так как плотность газа зависит от его давления, основное уравнение статики справедливо только для очень тонкого (бесконечно тонкого) слоя воздуха , в котором плотность воздуха почти не изменяется. На практике оно применимо, когда изменение высоты достаточно мало по отношению к приблизительной толщине атмосферы.
Приведение к уровню моря
Многие метеостанции рассылают так называемые «синоптические телеграммы», в которых указывается давление, приведённое к уровню моря (см. КН-01, METAR). Это делается для того, чтобы давление было сравнимо на станциях, расположенных на разных высотах, а также для нужд авиации. Приведённое давление используется также и на синоптических картах.
При приведении давления к уровню моря используют сокращенную формулу Лапласа:
То есть, зная давление и температуру на уровне , можно найти давление на уровне моря .
Вычисление давления на высоте по давлению на уровне моря и температуре воздуха :
где — давление Па на уровне моря [Па];
— молярная масса сухого воздуха, M = 0,029 кг/моль;
— ускорение свободного падения, g = 9,81 м/с²;
— универсальная газовая постоянная, R = 8,31 Дж/моль·К;
— абсолютная температура воздуха, К, , где — температура Цельсия, выражаемая в градусах Цельсия (обозначение: °C);
— высота, м.
На небольших высотах каждые 12 м подъёма уменьшают атмосферное давление на 1 мм рт. ст. На больших высотах эта закономерность нарушается[5].
Более простые расчёты (без учёта температуры) дают:
где — высота в километрах.
Измерения и расчёт показывают в полном согласии, что при подъёме над уровнем моря на каждый километр давление будет падать на 0,1 долю; то же самое относится и к спуску в глубокие шахты под уровень моря — при опускании на один километр давление будет возрастать на 0,1 своего значения.
Речь идёт об изменении на 0,1 от значения на предыдущей высоте. Это значит, что при подъёме на один километр давление уменьшается до 0,9 (точнее 0,87[прим 1]) от давления на уровне моря.
В ещё более грубом приближении, двукратному изменению давления соответствует изменение высоты на каждые пять километров.
В прогнозах погоды и сводках, распространяемых для населения через интернет и по радио, используется неприведённое давление, то есть, фактическое давление на уровне местности.
См. также
Примечания
Источники
- Давление Архивная копия от 20 декабря 2016 на Wayback Machine // Метеорологический словарь
- Атмосферное давление // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Положение о единицах величин, допускаемых к применению в Российской Федерации Архивная копия от 2 ноября 2013 на Wayback Machine Утверждено Постановлением Правительства РФ от 31 октября 2009 г. N 879.
- Перышкин А. В. Измерение атмосферного давления. Опыт Отто Герике // Физика. 7 класс / Е. Н Тихонова. — 16-е изд. — М.: Дрофа, 2013. — С. 190. — 189 с.
- Атмосферное давление. Класс!ная физика. Дата обращения: 9 июня 2015.
- Метеочувствительность: что это такое и как с ней бороться. РИА Новости. Дата обращения: 9 июня 2015. Архивировано 18 августа 2013 года.
- Смерч. pogoda.by. Дата обращения: 7 июня 2015.
- Изобары (в физике) // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Standard pressure (англ.). IUPAC. Дата обращения: 18 августа 2013. Архивировано 18 августа 2013 года.
- Барометрическая формула // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Сноски
- Формула предполагает температуру одинаковой на всех высотах. На самом же деле температура атмосферы меняется с высотой по довольно сложному закону. Тем не менее формула даёт неплохие результаты, и на высотах до 50-100 километров ею можно пользоваться. Так, нетрудно определить, что на высоте Эльбруса — около 5,6 км — давление упадёт примерно вдвое, а на высоте 22 км (рекордная высота подъёма стратостата с людьми) давление упадёт до 50 мм рт. ст.
Литература
- Хргиан А. Х. Физика атмосферы. — 2 изд. — М., 1958.
- Бургесс Э. К границам пространства, пер. с англ.. — М.: Изд. иностранной литературы, 1957. — 223 с.
Ссылки
 Медиафайлы по теме Атмосферное давление на Викискладе
Медиафайлы по теме Атмосферное давление на Викискладе- Атмосферное давление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- График изменения атмосферного давления при изменении высоты
