Алгоритм Кристофидеса
Алгоритм Кристофидеса или алгоритм Кристофидеса-Сердюкова — это алгоритм поиска приближённых решений задачи коммивояжёра для случаев, когда расстояния образуют метрическое пространство (симметричны и удовлетворяют неравенству треугольника)[1]. Алгоритм является аппроксимационным алгоритмом, который гарантирует, что решения находятся в пределах 3/2 от длины оптимального решения. Алгоритм назван именем Никоса Кристофидеса и Анатолия Ивановича Сердюкова, которые независимо друг от друга нашли его в 1976[2][3][4], и он обладает лучшим аппроксимационным коэффициентом, который был доказан для задачи коммивояжёра на метрических пространствах общего вида, хотя известны лучшие приближения для некоторых специальных случаев.
Алгоритм
Пусть будет представителем задачи коммивояжёра. То есть G является полным графом на множестве вершин V, а функция w назначает неотрицательные вещественные веса каждому ребру графа G. Согласно неравенству треугольника для любых трёх вершин u, v и x должно выполняться .
Алгоритм можно описать на псевдокоде следующим образом[1].
- Создаём минимальное остовное дерево T графа G.
- Пусть O будет набором вершин с нечётными степенями в T. Согласно лемме о рукопожатиях, O имеет чётное число вершин.
- Находим совершенное паросочетание M минимального веса в порождённом подграфе, заданным вершинами из O.
- Комбинируем рёбра M и T с образованием связного мультиграфа H, в котором каждая вершина имеет чётную степень.
- Образуем эйлеров цикл в H.
- Преобразуем цикл, найденный на предыдущем шаге, в гамильтонов цикл путём пропуска повторяющихся вершин (сокращение).
Аппроксимационный коэффициент
Стоимость решения, полученного алгоритмом, лежит в границах 3/2 от оптимального. Для доказательства этого факта предположим, что C является оптимальным обходом задачи коммивояжёра. Удаление ребра из C даёт стягивающее дерево, которое должно иметь вес, не меньший веса минимального стягивающего дерева, откуда следует, что . Далее нумеруем вершины O в циклическом порядке по C и делим C на два множества путей — одно имеет нечётные номера первых вершины в циклическом порядке, а второе имеет чётные номера. Каждый набор путей соответствует совершенному паросочетанию множества O, которое сочетает в пару две конечные точки каждого пути, а вес этого сочетания не превосходит веса путей. Поскольку эти два множества путей разбивают рёбра C, одно из этих двух множеств имеет максимум половину веса C, и благодаря неравенству треугольника их соответствующее паросочетание имеет вес, который также не менее половины веса C. Совершенное паросочетание минимального веса не может иметь больший вес, так что . Сложение весов T и M даёт вес эйлерова цикла, который не превосходит . Благодаря неравенству треугольника сокращение не увеличивает вес, так что вес результата также не превосходит [1].
Нижние границы
Существуют экземпляры задачи коммивояжёра, на которых алгоритм Кристофидеса находит решение, которое произвольно близко 3/2. Один из таких классов задач сформирован путём из n вершин с весами рёбер 1 вместе с набором рёбер, соединяющих вершины, отстоящие вдоль пути на два шага, с весами , где выбирается близким к нулю, но положительным. Все оставшиеся рёбра полного графа имеют расстояния, равные кратчайшим путям в этом подграфе. Тогда минимальное стягивающее дерево будет задано путём длины и только две нечётные вершины будут конечными точками пути и его совершенное паросочетание состоит из одного ребра с весом примерно n/2. Объединение дерева и паросочетания является циклом без сокращений вершин и весом примерно . Однако оптимальное решение использует рёбра весом вместе с двумя рёбрами веса 1, инцидентных концам пути, и его полный вес равен , что близко к n для малых значений . Отсюда мы получаем аппроксимационный коэффициент 3/2[5].
Пример
 | Дано: полный граф, веса рёбер которого удовлетворяют неравенству треугольника |
 | Вычисляем минимальное остовное дерево T |
 | Вычисляем множество вершин O с нечётной степенью в T |
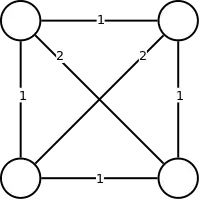 | Образуем подграф графа G, используя лишь вершины множества O |
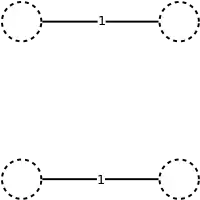 | Строим совершенное паросочетание минимального веса M в этом подграфе |
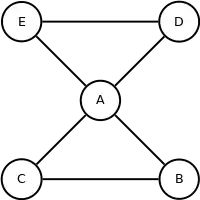 | Объединяем паросочетание и стягивающее дерево T ∪ M для образования эйлерова мультиграфа |
 | Вычисляем эйлеров обход |
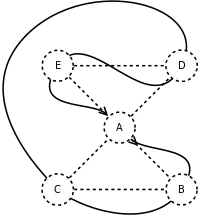 | Удаляем повторяющиеся вершины и получаем результирующий обход |
Примечания
- Goodrich, Tamassia, 2015, с. 513–514.
- Сердюков А. И. О некоторых экстремальных обходах в графах // Управляемые системы : журнал. — 1978. — Т. 17. — С. 76–79.
- van Bevern R., Slugina V. A. A historical note on the 3/2-approximation algorithm for the metric traveling salesman problem (англ.) // Historia Mathematica. — 2020. — doi:10.1016/j.hm.2020.04.003. — arXiv:2004.02437.
- Christofides N. Worst-case analysis of a new heuristic for the travelling salesman problem (англ.) // Management Sciences Research Report No. 388, Graduate School of Industrial Administration, Carnegie-Mellon University : технический отчёт. — 1976.
- Bläser, 2008, с. 517–519.
Литература
- Michael T. Goodrich, Roberto Tamassia. 18.1.2 The Christofides Approximation Algorithm // Algorithm Design and Applications. — Wiley, 2015.
- Markus Bläser. Metric TSP // Encyclopedia of Algorithms / Ming-Yang Kao. — Springer-Verlag, 2008. — ISBN 9780387307701.