Алгоритм Британского музея

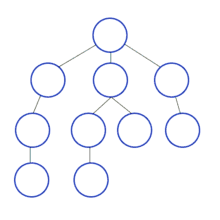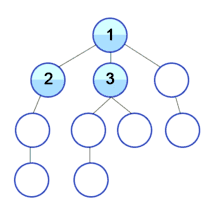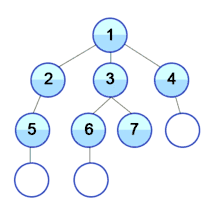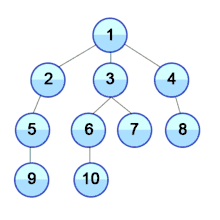
Алгоритм Британского музея заключается в переборе всех возможных вариантов, начиная с самого маленького по размеру, пока верное решение не будет найдено. Данный алгоритм почти не применим на практике, являясь лишь принципом, в теории применимым к любой задаче с большим числом возможных вариантов.

Например, с помощью алгоритма можно найти самую короткую программу, решающую поставленную задачу, следующим образом. Сначала создаются все возможные программы с исходным кодом длиной в один символ. Затем осуществляется проверка, решает ли каждая из программ задачу. (Такая проверка значительно затрудняется проблемой остановки). Если ни одна из программ не справляется с задачей, рассматриваются все программы длиной в два символа, три символа и так далее. В теории в результате искомая программа действительно будет найдена, однако на практике алгоритм будет работать чрезмерно долго (во многих случаях время работы может превысить продолжительность существования Вселенной).

Пользуясь аналогичными выкладками, алгоритм можно использовать для доказательства оптимизаций, теорем, тестирования систем распознавания языков и для иных целей.

Американские учёные Аллен Ньюэлл, Клифф Шоу и Герберт Саймон[1] нарекли данную процедуру «алгоритмом Британского музея», поскольку

«[идея] показалась им столь же безумной, как и попытка рассаживать обезьян перед печатными машинками в надежде, что они воспроизведут все книги из Британского музея»

См. также

Источники

Примечания
  1. Newell Allen, Shaw J. C., Simon Herbert A. Elements of a theory of human problem solving. // Psychological Review. — 1958. — Т. 65, № 3. — С. 151—166. — ISSN 0033-295X. — doi:10.1037/h0048495.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.