Адаптивный фильтр
Адаптивный фильтр — система с линейным фильтром, имеющим передаточную функцию, контролируемую переменными параметрами и средствами для установки этих параметров согласно оптимизационному алгоритму. Ввиду сложности оптимизационных алгоритмов почти все адаптивные фильтры являются цифровыми фильтрами. Адаптивные фильтры требуются для некоторых приложений, поскольку некоторые параметры желательной операции обработки (например, местоположение отражающих поверхностей в реверберирующем пространстве) заранее не известны или меняются. Адаптивный фильтр с замкнутой петлёй использует обратную связь в виде сигнала ошибки для оптимизации функции передачи.
Вообще говоря, адаптивный процесс с замкнутой петлёй вовлекает применение функции цены, которая является критерием оптимальности производительности фильтра, для использования в алгоритме, который определяет, как модифицировать передаточную функцию фильтра для минимизации цены на следующей итерации. Наиболее употребительной функцией цены является среднеквадратичное значение сигнала ошибки.
Так как мощность цифровых сигнальных процессоров возросла, адаптивные фильтры стали более распространёнными и теперь запросто используются в устройствах, таких как мобильные телефоны, и других устройствах коммуникации, камкодерах и цифровых камерах, а также в медицинском оборудовании мониторинга.
Пример приложения
Запись биения сердца (ЭКГ) может содержать шумы от сетей переменного тока. Точное значение частоты напряжения сети и его гармоники могут время от времени меняться.
Одним из способов удаления шума является фильтрация сигнала с помощью полосно-заграждающего фильтра по частоте сети и её окрестности, что может сильно испортить качество ЭКГ, поскольку биение сердца может иметь близкие к отсекаемой области частотные компоненты.
Чтобы обойти эти потенциальные потери информации, может быть использован адаптивный фильтр. Адаптивный фильтр мог бы принимать сигнал как от пациента, так и от сети и был бы способен отслеживать действительную частоту шума, как и его флуктуации, и вычитать шум из записи. Такая адаптивная техника в общем случае позволяет применять фильтры с более узкой полосой отсечения, что в данном случае означает более точный выходной сигнал для медицинских целей[1][2].
Блочная диаграмма
Идея адаптивного фильтра с замкнутой петлёй заключается в том, что переменный фильтр настраивается, пока ошибка (разница между выходом фильтра и желаемым сигналом) не станет минимальной. Фильтр минимальной среднеквадратичной ошибки (фильтр МСК, англ. Least Mean Squares, LMS) и рекурсивный фильтр среднеквадратичной ошибки (фильтр РСК, англ. Recursive Least Square, RLS) являются адаптивными фильтрами.
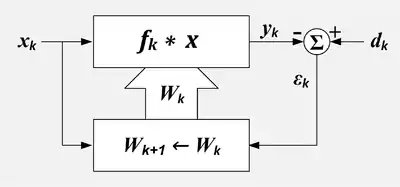 Адаптивный фильтр. k = номер экземпляра, x = входная величина, X = набор последних значений x, d = желаемый вход, W = набор коэффициентов фильтрации, ε = ошибка выхода, f = ответ фильтра, * = свёртка, Σ = суммирование, верхний блок=линейный фильтр, нижний блок=алгоритм адаптации
Адаптивный фильтр. k = номер экземпляра, x = входная величина, X = набор последних значений x, d = желаемый вход, W = набор коэффициентов фильтрации, ε = ошибка выхода, f = ответ фильтра, * = свёртка, Σ = суммирование, верхний блок=линейный фильтр, нижний блок=алгоритм адаптации
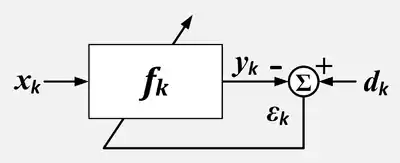
Существует два входных сигнала адаптивного фильтра: dk и xk, которые иногда называются главным входом и контрольной входной величиной соответственно[3].
- который включает желаемый сигнал плюс нежелательные помехи и
- который включает сигналы, которые коррелируют с некоторыми нежелательными помехами в .
- k представляет дискретный номер экземпляра.
Фильтр контролируется набором L+1 коэффициентов или весов.
- представляют набор векторов или весов, которые контролируют фильтр в момент времени k.
- где относится к -ому весу в момент k.
- представляют изменения в весах, которые возникают как результат поправки в момент времени k.
- Эти изменения будут применены после момента k и до того, как они использованы в момент k+1.
Выход обычно равен , но он может быть или даже коэффициентами фильтра[4].
Входные сигналы определяются следующим образом:
- где:
- g = желаемый сигнал,
- g' = сигнал, коррелирующий с желаемым сигналом g ,
- u = нежелательный сигнал, добавленный к g , но не коррелирующий с g или g'
- u' = сигнал, коррелирующий с нежелательным сигналом u , но не коррелирующий с g или g' ,
- v = нежелательный сигнал (обычно, случайный шум), не коррелирующий с g , g' , u, u' или v' ,
- v' = нежелательный сигнал (обычно, случайный шум), не коррелирующей с g , g' , u, u' или v.
Выходные сигналы определяются следующим образом:
- .
- где
- = выход фильтра, если входом служит только g' ,
- = выход фильтра, если входом служит только u' ,
- = выход фильтра, если входом служит только v' .
КИХ фильтр с секционной линией задержки
Если переменный фильтр имеет секционную линию задержки со структурой, имеющей конечную импульную характеристику (КИХ, англ. Finite Impulse Response, FIR), тогда импульсный ответ равен коэффициентам фильтра. Выход фильтра задаётся выражением
-
- где относится к -ому весу в момент k.
Идеальный случай
В идеальном случае . Все нежелательные сигналы в представлены значениями . Значение состоит полностью из сигнала, коррелирующего с нежелательным сигналом в .
Выход переменного фильтра в идеальном случае равен
- .
Сигнал ошибки или функция цены является разностью между и
- . Желаемый сигнал gk проходит сквозь без изменений.
Сигнал ошибки минимизируется в смысле среднего квадратичного, когда минимизируется. Другими словами, является лучшей среднеквадратичной оценкой . В идеальном случае и и всё, что остаётся после вычитания, это , который является неизменённым желаемым сигналом с удалёнными всеми нежелательными сигналами.
Компоненты сигнала в контрольной входной величине
В некоторых случаях контрольная входная величина включает компоненты желаемого сигнала. Это означает g' ≠ 0.
Полное удаление нежелательных помех взаимного влияния невозможно в этом случае, но улучшение сигнала по уровню помех возможно. Выход будет
- . Желаемый сигнал будет модифицирован (обычно будет уменьшен).
Отношение выходного сигнала к помехе взаимного влияния имеет простую формулу, называемую обращением мощности.
- .
- где
- = отношение выходного сигнала и помехи взаимного влияния.
- = отношение контрольного сигнала и помехи взаимного влияния.
- = частота в z-области.
- где
Эта формула означает, что отношение выходного сигнала и помехи взаимного влияния на конкретной частоте противоположно отношению контрольного сигнала и помехи взаимного влияния[5].
Пример: Ресторан быстрого питания имеет подъездное окно для обслуживания автомобилистов. Перед тем как добраться до окна, пользователи помещают свой заказ, проговаривая его в микрофон. Микрофон воспринимает также шум двигателя и окружающей среды. Этот микрофон воспринимает основной сигнал. Сила сигнала от голоса пользователя и от двигателя одинаковы. Трудно для сотрудников ресторана понять пользователя. Чтобы уменьшить величину помехи взаимного влияния в главном микрофоне, второй микрофон располагается в месте, где он воспринимает звук двигателя. Также он воспринимает и голос пользователя. Этот микрофон является источником контрольного сигнала. В этом случае шум двигателя в 50 раз больше силы голоса заказчика. После удаления шума отношение главного сигнала к помехе взаимного влияния будет улучшен с 1:1 до 50:1.
Адаптивное линейное объединяющее устройство
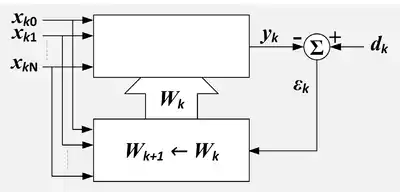 Адаптивное линейное объединяющее устройство с объединяющим устройством и процессором адаптации. k = номер экземпляра, n=индекс входной переменной, x = контрольные входные величины, d = желаемый вход, W = набор коэффициентов, ε = ошибка выхода, Σ = суммирование, верхний блок=линейное объединяющее устройство, нижний блок= алгоритм адаптации.
Адаптивное линейное объединяющее устройство с объединяющим устройством и процессором адаптации. k = номер экземпляра, n=индекс входной переменной, x = контрольные входные величины, d = желаемый вход, W = набор коэффициентов, ε = ошибка выхода, Σ = суммирование, верхний блок=линейное объединяющее устройство, нижний блок= алгоритм адаптации.
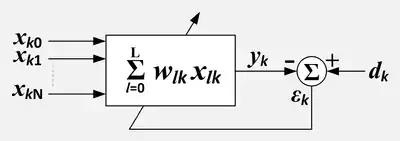
Адаптивное линейное комбинирующее устройство (АЛК, англ. Adaptive Linear Combiner, ALC) похож на адаптивный КИХ фильтр с секционной линией задержки, за исключением того, что не имеется никаких предположений о связи между значениями X. Если X значения получены как выход секционной линии задержки, то комбинация секционной линии задержки и АЛК могла бы составлять адаптивный фильтр. Однако значения X могут быть массивом пикселей, или они могут быть выходами множественных секционных линий задержки. АЛК находит применение как адаптивный формирователь лучей для массивов гидрофонов или антенн.
-
- где означает -ый вес в момент времени k.
Алгоритм МСК
Если переменный фильтр имеет структуру КИХ с секционной линией задержки, то алгоритм обновления МСК особенно прост. Обычно после каждого поступления элемента коэффициенты КИХ фильтра пересчитываются следующим образом[6]:
- для
-
- μ называется множителем сходимости.
Алгоритм МСК не требует, чтобы значения X имели какие-либо связи. Поэтому он может быть использован для линейного объединяющего устройства, как и для КИХ фильтра. В этом случае формула обновления записывается следующим образом:
Эффект алгоритма МСК заключается в том, что в каждый момент времени k делается небольшое изменение весов. Направление изменения выбирается так, чтобы уменьшить ошибку, если бы алгоритм был применён в момент k. Величина изменения каждого веса зависит от μ, ассоциированного значения X и ошибки в момент k. Веса, дающие больший вклад в выход изменяются больше. Если ошибка равна нулю, никаких изменений в весах не делается. Если ассоциированное значение X нулевое, то изменение весов не даст результатов, так что они не меняются.
Сходимость
Значение μ контролирует, насколько быстро и как хорошо алгоритм сходится к оптимальным коэффициентам фильтра. Если μ слишком велико, алгоритм не сходится. Если μ слишком мало, алгоритм сходится медленно и может оказаться неспособным отслеживать изменения. Если μ большое, но не слишком большое, чтобы расходиться, алгоритм достигает стационарного состояния быстро, но постоянно делает чрезмерные изменения в векторе весов. Иногда μ делается сначала большим для быстрой сходимости, а затем оно постепенно уменьшается для минимизации «перелёта».
Уидроу и Сернс утверждали в 1985, что не знают доказательства, что алгоритм МСК сходится во всех случаях[7].
Однако при некоторых предположениях о стационарности и независимости можно показать, что алгоритм сходится, если
- где
- = сумма всех значений входа
- где
- является среднеквадратичным (СК, англ. Root mean square, RMS) значением -го входа
В случае фильтра с секционной линией задержки каждый вход имеет одно и то же значение СК, поскольку они являются одним значением, полученным в результате задержки. В этом случае полное значение сигнала равно
- где
- является значением СК входного потока [7].
- где
Это приводит к нормализованному алгоритму МСК:
и в этом случае критерием сходимости становится .
Приложения адаптивных фильтров
- Активное шумоподавление
- Предсказание сигнала
- Адаптивная система подавления обратной акустической связи
- Эхоподавление
Реализации фильтра
- Фильтр минимальной среднеквадратичной ошибки
- Рекурсивный фильтр минимальной среднеквадратичной ошибки
- Блочный фильтр с адаптацией в частотной области с задержками
См. также
- Двумерные адаптивные фильтры
- Фильтр (обработка сигналов)
- Фильтр Калмана
- Ядерный адаптивный фильтр
- Линейное предсказание
- Винеровское оценивание
- Уравнение Винера — Хопфа
Примечания
- Thakor, Zhu, 1991, с. 785–794.
- Widrow, Stearns, 1985, с. 329.
- Widrow, Stearns, 1985, с. 304.
- Widrow, Stearns, 1985, с. 212.
- Widrow, Stearns, 1985, с. 313.
- Thakor, Zhu, 1991, с. 786.
- Widrow, Stearns, 1985, с. 103.
Литература
- Thakor N.V., Yi-Sheng Zhu. Applications of adaptive filtering to ECG analysis: noise cancellation and arrhythmia detection // IEEE Transactions on Biomedical Engineering. — 1991. — Август (т. 38, вып. 8). — ISSN 0018-9294. — doi:10.1109/10.83591.
- Bernard Widrow, Samuel D. Stearns. Adaptive Signal Processing. — 1st. — Englewood Cliffs, NJ: Prentice-Hall, 1985. — ISBN 0-13-004029-0.
- Monson H. Hayes. Statistical Digital Signal Processing and Modeling. — Wiley, 1996. — ISBN 0-471-59431-8.
- Simon Haykin. Adaptive Filter Theory. — Prentice Hall, 2002. — ISBN 0-13-048434-2.
