RIPEMD-128
RIPEMD-128 (англ. RACE Integrity Primitives Evaluation Message Digest) — криптографическая хеш-функция, разработанная Гансом Доббертином, Антоном Боселаерсом и Бартом Пренелем в 1996 году.
| RIPEMD-128 | |
|---|---|
| Разработчики | Ганс Доббертин, Антон Боселаерс и Барт Пренель |
| Создан | 1996 |
| Стандарты | ISO/IEC 10118-3:2004 |
| Размер хеша | 128 бит |
| Число раундов | 4 |
| Тип | хеш-функция |
История
RIPEMD представляет собой несколько хеш-функций, относящихся к семейству MD-SHA. Первой из них была RIPEMD-0, рекомендованная в 1992 году консорциумом для Оценки примитивов целостности RACE (англ. RACE Integrity Primitives Evaluation, RIPE) в качестве улучшенной версии алгоритма MD4[1]. Криптоанализ, проведённый Гансом Доббертином, показал, что данный алгоритм не является безопасным в плане наличия коллизий, что позже было подтверждено найденными уязвимостями[2]. RIPEMD-128 (совместно с 160-битной версией, RIPEMD-160) была представлена как замена оригинальной RIPEMD, которая тоже была 128-битной. Были разработаны и другие версии алгоритма, с большей длиной хеша: RIPEMD-256 и RIPEMD-320 (соответственно 256- и 320-битные).
Другой причиной перехода к алгоритмам, выдающим результат с большим количеством бит, было стремительное развитие вычислительной техники (согласно закону Мура). Имеющиеся в то время алгоритмы с каждым годом становились всё более и более уязвимыми для коллизионных атак путём полного перебора. Тем не менее, RIPEMD-128 нашла своё применение в некоторых банковских приложениях[3]. В 2004 году была стандартизирована (ISO/IEC 10118-3:2004).
Алгоритм
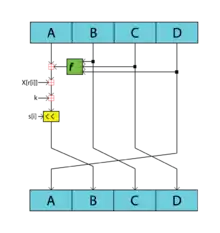
Для произвольного входного сообщения хеш-функция генерирует 128-разрядное хеш-значение — дайджест сообщения. Алгоритм основан на алгоритме хеширования MD4. Хеширование MD4 состоит из 48 операций, содержащих применение нелинейных булевых функций, сгруппированных в 3 раунда по 16 операций. В алгоритме RIPEMD-128 увеличено число раундов до 4. Кроме того, используются другие булевы функции и значения констант[3]. В алгоритме параллельно выполняются две линии (потока), которые условно разделяют на Левую и Правую.
Алгоритм состоит из нескольких основных шагов:
1. Добавление недостающих битов
Алгоритм оперирует с блоками данных длиной 512 бит, входное сообщение предварительно приводится к требуемому размеру. Для начала, вне зависимости от начальной длины сообщения, к нему добавляется один бит, равный 1. Далее к нему добавляются биты, равные 0, до тех пор, пока длина получаемой последовательности не станет равной 448 бит по модулю 512. В результате расширения, до длины в 512 бит модифицированному сообщению недостаёт ровно 64 бит. На этом шаге к нему может быть добавлено от 1 до 512 бит.
2. Добавление длины сообщения
На следующем шаге к 448-битному полученному сообщению добавляется длина исходного сообщения (до применения первого шага) в 64-битном представлении. В случае, если исходная длина сообщения превышает 264 бит, то от её битовой длины используется только младшие 64 бита. Причём, длина исходного сообщения добавляется в виде двух 32-битных слов: первым добавляются младшие 32 бита, затем старшие. После этого этапа длина модифицированного сообщения становится равной 512 битам. Его также можно представить в виде 16 32-битных слов.
a. Порядок слов в сообщении
Для определения порядка 32-битных слов в сообщении в каждом раунде используются различные комбинации функций перестановок.
Определим функцию перестановки :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 7 | 14 | 13 | 1 | 10 | 6 | 15 | 3 | 12 | 0 | 9 | 5 | 2 | 14 | 11 | 8 |
А также функцию перестановки :
В каждом раунде порядок определяется следующим образом:
| Линия | Раунд 1 | Раунд 2 | Раунд 3 | Раунд 4 |
|---|---|---|---|---|
| Левая | ||||
| Правая |
б. Булевы функции
В каждом раунде для каждой линии применяются определённые булевы функции.
Определим нелинейные побитовые булевы функции:
В каждом раунде в зависимости от линии будут применяться:
| Линия | Раунд 1 | Раунд 2 | Раунд 3 | Раунд 4 |
|---|---|---|---|---|
| Левая | ||||
| Правая |
в. Сдвиги
Для обеих линий применяются следующие сдвиги ():
| Раунд | X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 11 | 14 | 15 | 12 | 5 | 8 | 7 | 9 | 11 | 13 | 14 | 15 | 6 | 7 | 9 | 8 |
| 2 | 12 | 13 | 11 | 15 | 6 | 9 | 9 | 7 | 12 | 15 | 11 | 13 | 7 | 8 | 7 | 7 |
| 3 | 13 | 15 | 14 | 11 | 7 | 7 | 6 | 8 | 13 | 14 | 13 | 12 | 5 | 5 | 6 | 9 |
| 4 | 14 | 11 | 12 | 14 | 8 | 6 | 5 | 5 | 15 | 12 | 15 | 14 | 9 | 9 | 8 | 6 |
г. Константы
В качестве констант (), применяемых в алгоритме, используются целые части следующих вещественных чисел:
| Линия | Раунд 1 | Раунд 2 | Раунд 3 | Раунд 4 |
|---|---|---|---|---|
| Левая | ||||
| Правая |
4. Выполнение хеширования
После задания всех исходных функций и констант, приведению сообщения к требуемому размеру, можно переходить к выполнению алгоритма. Выполнение алгоритма происходит по двум параллельным путям (линиям). Обработка сообщения происходит словами по 16 слов в 32 бита.
На каждом шаге для каждой из линий выполняется следующая операция:
где обозначает циклический сдвиг на позиций.
Скорость работы
В таблице для сравнения приведены скорости выполнения MD-подобных функций. Тестовые программы были написаны на языке ассемблера и Си, с использованием оптимизаций для тестовой машины:[4]
| Алгоритм | Мбит/сек — asm | Мбит/сек — С | Относительная производительность |
|---|---|---|---|
| RIPEMD-128 | 77.6 | 35.6 | 1.00 |
| RIPEMD-160 | 45.3 | 19.3 | 0.58 |
| SHA-1 | 54.9 | 21.2 | 0.71 |
| MD5 | 136.2 | 59.7 | 1.76 |
| MD4 | 190.6 | 81.4 | 2.46 |
Независимое исследование, проведённое позднее, показало довольно схожие результаты. В замере была использована Си++ библиотека Crypto++:[5]
| Алгоритм | Мбит/сек | Циклов на байт | Относительная производительность |
|---|---|---|---|
| RIPEMD-128 | 153 | 11.4 | 1.00 |
| RIPEMD-160 | 106 | 16.5 | 0.69 |
| RIPEMD-256 | 158 | 11.1 | 1.03 |
| RIPEMD-320 | 110 | 15.9 | 0.72 |
| SHA-1 | 153 | 11.4 | 1.00 |
| MD5 | 255 | 6.8 | 1.67 |
Криптостойкость
В криптографии различают два основных вида атак на криптографические хеш-функции: атаку нахождения прообраза — попытку отыскать сообщение с заданным значением хеша, и коллизионную атака — поиск двух различных входных блоков криптографической хеш-функции, производящих одинаковые значения хеш-функции, то есть коллизию хеш-функции.
Алгоритм RIPEMD-128, как и другие алгоритмы семейства RIPEMD, включая оригинальный первый, считаются устойчивыми к атаке нахождения прообраза. Для RIPEMD-128 вычислительная сложность нахождения первого прообраза составляет 2128, что совпадает с максимальным для её битовой длины значением — отыскание требует полного перебора:[6]
| Алгоритм | Сложность нахождения прообраза | Лучшая атака (раунды) |
|---|---|---|
| RIPEMD (original) | 2128 | 35 из 48 |
| RIPEMD-128 | 2128 | 35 из 64 |
| RIPEMD-160 | 2160 | 31 из 80 |
Для сокращённого варианта RIPEMD-128 существуют алгоритмы нахождения первого прообраза, требующие меньшей сложности:[7]
| Раунды | Сложность отыскания | Источник |
|---|---|---|
| 33 | 2124,5 | Статья[6] |
| 35 | 2121 | Статья[6] |
| 36 | 2126,5 | Статья[8] |
Оригинальная RIPEMD не была безопасной с точки зрения коллизий. О коллизии стало известно в 2004 году[2], в 2005 году вышла соответствующая статья, посвящённая криптоанализу алгоритма[9]. Так как любая криптографическая хеш-функция по определению уязвима для атаки «дней рождения», то сложность подбора не может превышать 2N/2 для N-битной хеш-функции. Однако, 128-битная RIPEMD может быть «сломана» за время 218, что гораздо меньше соответствующего ей значения 264.
Полная RIPEMD-128 теоретически может быть «сломана». Коллизионная атака имеет сложность порядка 261.57 (против необходимой 264). В то время как сокращённый вариант подвержен более успешным атакам:
| Цель | Раунды | Сложность отыскания | Источник |
|---|---|---|---|
| Функция сжатия | 48 | 240 | Статья[7] |
| Функция сжатия | 60 | 257.57 | Статья[1] |
| Функция сжатия | 63 | 259.91 | Статья[1] |
| Функция сжатия | Полная (64) | 261.57 | Статья[1] |
| Функция хеширования | 38 | 214 | Статья[7] |
128-битный выход функции, который не казался достаточно защищённым в ближайшей перспективе[3], как раз и послужил поводом для перехода к RIPEMD-160. Для неё известны лишь коллизионные атаки на сокращённый вариант (48 из 80 раундов, 251 времени)[10].
Примеры
RIPEMD128("") = "cdf26213a150dc3ecb610f18f6b38b46"
RIPEMD128("a") = "86be7afa339d0fc7cfc785e72f578d33"
RIPEMD128("abc") = "c14a12199c66e4ba84636b0f69144c77"
Примеры, демонстрирующие лавинный эффект:
RIPEMD128("aaa100") = "5b250e8d7ee4fd67f35c3d193c6648c4"
RIPEMD128("aaa101") = "e607de9b0ca4fe01be84f87b83d8b5a3"
Ссылки
- Страница хеш-функций семейства RIPEMD (описание, исходные коды)
- Основная статья разработчиков
Примечания
- Franck Landelle, Thomas Peyrin. Cryptanalysis of Full RIPEMD-128. — Division of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore, 2013.
- Xiaoyun Wang, Dengguo Feng, Xuejia Lai, Hongbo Yu. Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD. — Dept. of Computer Science and Engineering, Shanghai Jiaotong University, Shanghai, China, 2004.
- Hans Dobbertin, Antoon Bosselaers, Bart Preneel. RIPEMD-160: A Strengthened Version of RIPEMD. — 1996.
- Bart Preneel, Hans Dobbertin, Antoon Bosselaers. The Cryptographic Hash Function RIPEMD-160. — 1997.
- Wei Dai. Speed Comparison of Popular Crypto Algorithms. Дата обращения: 22 января 2017.
- Chiaki Ohtahara, Yu Sasaki, Takeshi Shimoyama. Preimage Attacks on Step-Reduced RIPEMD-128 and RIPEMD-160. — 2011.
- Florian Mendel, Tomislav Nad, Martin Schläffer. Collision Attacks on the Reduced Dual-Stream Hash Function RIPEMD-128. — 2012.
- Lei Wang, Yu Sasaki, Wataru Komatsubara, Kazuo Ohta, Kazuo Sakiyama. (Second) Preimage Attacks on Step-Reduced RIPEMD/RIPEMD-128 with a New Local-Collision Approach. — 2011.
- Xiaoyun Wang, Xuejia Lai, Dengguo Feng, Hui Chen, Xiuyuan Yu. Cryptanalysis of the Hash Functions MD4 and RIPEMD. — 2005. Архивировано 3 марта 2019 года.
- Florian Mendel, Norbert Pramstaller, Christian Rechberger, Vincent Rijmen. On the Collision Resistance of RIPEMD-160. — 2006.
