Коллизия хеш-функции
Колли́зия хеш-фу́нкции — два различных входных блока данных и для хеш-функции таких, что
Коллизии существуют для большинства хеш-функций, но для «хороших» хеш-функций частота их возникновения близка к теоретическому минимуму. В некоторых частных случаях, когда множество различных входных данных конечно, можно задать инъективную хеш-функцию, по определению не имеющую коллизий. Однако для хеш-функций, принимающих вход переменной длины и возвращающих хеш постоянной длины (таких как MD5), коллизии обязаны существовать, поскольку хотя бы для одного значения хеш-функции соответствующее ему множество входных данных (полный прообраз) будет бесконечно — и любые два набора данных из этого множества образуют коллизию.
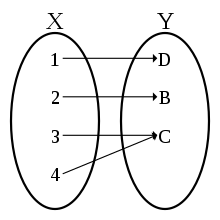
Пример
Рассмотрим в качестве примера хеш-функцию , определённую на множестве целых чисел. Её область значений состоит из 19 элементов (кольца вычетов по модулю 19), а область определения — бесконечна. Так как множество прообразов заведомо больше множества значений, коллизии обязаны существовать.
Построим коллизию для этой хеш-функции для входного значения 38, хеш-сумма которого равна нулю. Так как функция — периодическая с периодом 19, то для любого входного значения y, значение y + 19 будет иметь ту же хеш-сумму, что и y. В частности, для входного значения 38 той же хеш-суммой будут обладать входные значения 57, 76, и т. д. Таким образом, пары входных значений (38,57), (38,76) образуют коллизии хеш-функции .
Коллизии криптографических хеш-функций
Так как криптографические хеш-функции используются для подтверждения неизменности исходной информации, то возможность быстрого отыскания коллизии для них обычно равносильна дискредитации. Например, если хеш-функция используется для создания цифровой подписи, то умение находить для неё коллизии фактически равносильно умению подделывать цифровую подпись. Поэтому мерой криптостойкости хеш-функции считается вычислительная сложность нахождения коллизии. В идеале не должно существовать способа отыскания коллизий более быстрого, чем полный перебор. Если для некоторой хеш-функции находится способ получения коллизий существенно более быстрый, чем полный перебор, то эта хеш-функция перестаёт считаться криптостойкой и использоваться для передачи и хранения секретной информации. Теоретические и практические вопросы отыскания и использования коллизий ежегодно обсуждаются в рамках международных конференций (таких как CRYPTO или ASIACRYPT), на большом количестве ресурсов Интернета, а также во множестве публикаций.
Свойства криптографических хеш-функций
Для того, чтобы хеш-функция H считалась криптографически стойкой, она должна удовлетворять трём основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
- Необратимость: для заданного значения хеш-функции m должно быть практически невозможно найти блок данных , для которого .
- Стойкость к коллизиям первого рода: для заданного сообщения M должно быть практически невозможно подобрать другое сообщение N, для которого .
- Стойкость к коллизиям второго рода: должно быть практически невозможно подобрать пару сообщений , имеющих одинаковый хеш.
Использование коллизий для взлома
В качестве примера можно рассмотреть простую процедуру аутентификации пользователя:
- при регистрации в системе пользователь вводит свой пароль, к которому применяется некоторая хеш-функция, значение которой записывается в базу данных;
- при каждом вводе пароля, к нему применяется та же хеш-функция, а результат сравнивается с тем, который записан в БД.
При таком подходе, даже если злоумышленник получит доступ к базе данных, он не сможет восстановить исходные пароли пользователей (при условии необратимости используемой хеш-функции). Однако, если злоумышленник умеет находить коллизии для используемой хеш-функции, ему не составит труда найти поддельный пароль, который будет иметь ту же хеш-сумму, что и пароль пользователя.
Можно использовать коллизии для подделки сообщений: информация о валютных операциях, к примеру, часто шифруется посредством хеш-функций; злоумышленник, обладая методом нахождения коллизий этой хеш-функции, может заменить сообщение поддельным и тем самым повлиять на ход валютной операции.
Схожим образом можно использовать коллизии для подделки цифровых подписей и сертификатов.
Защита от использования коллизий
Существует ряд методов защиты от взлома, защиты от подделки паролей, подписей и сертификатов, даже если злоумышленнику известны методы построения коллизий для какой-либо хеш-функции.
Одним из методов является добавление «соли», то есть добавление некоторой последовательности символов к хешируемым данным, применяемое, например, при хранении UNIX-паролей. При этом та же «соль» добавляется также и к получаемому хешу, что существенно повышает сложность одновременного построения коллизий первого рода к группе паролей, так как каждый в этой группе должен начинаться со своего собственного (уникального) значения «соли». Однако, «соль» не усложняет атаку на каждый пароль в отдельности.
Другим популярным, но неработающим методом является конкатенация хешей, получаемых от двух различных хеш-функций. Считается, что при этом, чтобы подобрать коллизии к хеш-функции , являющейся конкатенацией хеш-функций и , необходимо знать методы построения коллизий и для , и . При этом есть исследования, показывающие, что использование конкатенаций хешей незначительно усиливает стойкость регулирующего хеша к коллизиям, причём не важно, как сильно отличаются хеш-функции друг от друга[1]. Если одна из хеш-функций достаточно слабая, чтобы найти в ней коллизию, вторая не сможет усилить результирующий хеш.
Методы поиска коллизий
Одним из самых простых и универсальных методов поиска коллизий является атака «дней рождения». С помощью этой атаки отыскание коллизии для хеш-функции разрядности битов потребует в среднем около операций. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к .
Кроме того, существует атака удлинением сообщения, которая для известного значения позволяет вычислить , где обозначает конкатенацию. Атака расширения для некоторых хеш-функций работает даже при обеспечении стойкости к коллизиям первого рода, стойкости к коллизиям второго рода, а также свойства необратимости. Подразумевается, что нет необходимости знать , а достаточно знать лишь его хеш. Таким образом можно, например, дописывать дополнительную информацию к чужому сообщению. Для предотвращения этой атаки используют различные методы: добавляют дополнительный раунд при хешировании, отличный от предыдущих; применяют многократное хеширование; или используют комбинацию предыдущих двух методов.
Но атаку расширения можно рассмотреть и с другой стороны: если у нас есть некоторое сообщение , и хеш-функция уязвима для атаки расширения, то легко можно найти коллизию первого рода: , , , то есть нарушается свойство стойкости к коллизиям первого рода.
Большая часть современных хеш-функций имеют одинаковую структуру, основанную на разбиении входного текста на блоки и последующем итерационном процессе, в котором на каждой итерации используется некоторая функция , где x — очередной блок входного текста, а y — результат предыдущей операции. Однако такая схема несовершенна, так как, зная функцию , можно проводить анализ данных в промежутках между итерациями, что облегчает поиск коллизий.
Часто нахождению коллизий хеш-функций предшествует нахождение её псевдоколлизий, то есть двух разных значений начального буфера, которые для одного и того же сообщения дают равные значения хеш-функции.
Коллизии хеш-функций MD4 и MD5
В 1996 году Ганс Доббертин нашёл псевдоколлизии в MD5, используя определённые инициализирующие векторы, отличные от стандартных. Оказалось, что можно для известного сообщения построить второе, такое, что оно будет иметь такой же хеш, как и исходное. C точки зрения математики это означает, что MD5(IV,L1) = MD5(IV,L2), где IV — начальное значение буфера, а L1 и L2 — различные сообщения.
В 2004 году китайские исследователи Ван Сяоюнь (Wang Xiaoyun), Фэн Дэнго (Feng Dengguo), Лай Сюэцзя (Lai Xuejia) и Юй Хунбо (Yu Hongbo) объявили об обнаруженной ими уязвимости в алгоритме, позволяющей за небольшое время (1 час на сервере IBM p690) находить коллизии.
В 2005 году исследователи Ван Сяоюнь и Юй Хунбо из университета Шаньдуна в Китае, опубликовали алгоритм для поиска коллизий в хеш-функции MD5, причём их метод работает для любого инициализирующего вектора, а не только для вектора, используемого по стандарту. Применение этого метода к MD4 позволяет найти коллизию меньше чем за секунду. Он также применим и к другим хеш-функциям, таким как RIPEMD и HAVAL.
В 2008 году Сотиров Александр, Марк Стивенс (Marc Stevens), Якоб Аппельбаум (Jacob Appelbaum) опубликовали на конференции 25th Chaos Communication Congress статью, в которой показали возможность генерирования поддельных цифровых сертификатов, на основе использования коллизий MD5.
Коллизии хеш-функции SHA-1
В январе 2005 года Винсент Рэймен и Elisabeth Oswald опубликовали сообщение об атаке на усеченную версию SHA-1 (53 раунда вместо 80), которая позволяет находить коллизии меньше, чем за 280 операций.
В феврале 2005 года Ван Сяоюнь, Лиза Инь Ицюнь и Юй Хунбо представили атаку на полноценный SHA-1, которая требует менее 269 операций.
В августе 2005 года на CRYPTO 2005 эти же специалисты представили улучшенную версию атаки на полноценный SHA-1, с вычислительной сложностью в 263 операций. В декабре 2007 года детали этого улучшения были проверены Мартином Кохраном.
Кристоф де Каньер и Кристиан Рехберг позже представили усовершенствованную версию атаки на SHA-1, за что были удостоены награды за лучшую статью на конференции ASIACRYPT 2006. Ими была представлена двух-блоковая коллизия на 64-раундовый алгоритм с вычислительной сложностью около 235 операций.
Ввиду того, что теоретические атаки на SHA-1 оказались успешными, NIST планирует полностью отказаться от использования SHA-1 в цифровых подписях.
Коллизии других хеш-функций
Хеш функции RIPEMD и HAVAL также являются уязвимыми для алгоритма поиска коллизий MD5, опубликованного Ван Сяоюнь (Wang Xiaoyun), Фен Дэнгуо (Feng Dengguo), Лай Сюэцзя (Lai Xuejia) и Юй Хунбо (Yu Hongbo) в 2004 году.
Для второй модификации хеш-функции WHIRLPOOL, называемой Whirlpool-T, на 2009 год не предложено алгоритмов поиска коллизий или псевдоколлизий; существенным ограничением для их нахождения является сложность самой функции и большая длина (512 бит) выходного ключа.
Хеш-функция ГОСТ Р 34.10-2001 по криптостойкости мало отличается от ГОСТ Р 34.10-94, нахождение коллизий для которой сводится к вычислению дискретного логарифма в группе точек эллиптической кривой с предположительно экспоненциальной сложностью. Например, для 256-битных параметров дискретное логарифмирование с помощью ρ-метода или λ-метода Полларда потребует выполнения около операций.
Разрешение коллизий в хеш-таблицах
Коллизии осложняют использование хеш-таблиц, так как нарушают однозначность соответствия между хеш-кодами и данными. Тем не менее, существуют специальные методики для преодоления возникающих сложностей:
- Метод цепочек: Технология сцепления элементов (chaining) состоит в том, что элементы множества, которым соответствует одно и то же хеш-значение, связываются в цепочку-список. В позиции номер i хранится указатель на голову списка тех элементов, у которых хеш-значение ключа равно i; если таких элементов в множестве нет, в позиции i записан NULL.
- Открытая адресация: В отличие от хеширования с цепочками, при открытой адресации никаких списков нет, а все записи хранятся в самой хеш-таблице. Каждая ячейка таблицы содержит либо элемент динамического множества, либо NULL.
- Исключение коллизий: В отличие от двух предыдущих методов, наличие коллизий в хэш-таблице исключается на этапе добавления элементов. Хэш-кодом, адресуемого элемента является хэш информации + случайное значение. Если хэш код уже есть в таблице, случайное значение перегенерируется, с повторным добавлением, в хэш-таблицу - элемента с другим хэшем. Таким образом, наличие коллизий исключается, и элементы можно найти по уникальным их хэшам, которые их адресуют - однозначно, в хэш-таблице.
Примечания
См. также
Ссылки
- Брюс Шнайер, Криптоанализ MD5 и SHA
- Cryptography Research, Hash Collision Q&A ( (англ.))
- Creating a rogue CA certificate, Alexander Sotirov, подделывание сертификатов на основе MD5 ( (англ.))
- International Association for Cryptologic Research Website
- Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD, Xiaoyun Wang and Dengguo Feng and Xuejia Lai and Hongbo Yu ( (англ.))
- Improved Collision Attack on Hash Function MD5, very technical ( (англ.))
- NIST Comments on Cryptanalytic Attacks on SHA-1, комментарий NIST об атаках на SHA-1 ( (англ.))
- Computer Algorithm Tutor
Литература
- Брюс Шнайер (Bruce Schneier), «Прикладная криптография», 2е издание, ISBN 0-471-11709-9, гл.18, Однонаправленные хеш-функции
- Росс Андерсон (Ross Anderson), «Security Engineering» ( (англ.)), Wiley, ISBN 0-471-38922-6