Функция Леонтьева
В экономической теории функция Леонтьева — производственная функция (либо функция полезности), в которой факторы производства использованы в фиксированных пропорциях, поскольку факторы являются абсолютными комплементами. Функция названа в честь американского экономиста российского происхождения Василия Леонтьева. Функция Леонтьева является предельным случаем Функции CES — класса функций, обладающих свойством постоянной эластичности замещения.
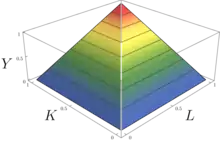
В простейшем случае с двумя факторами производства имеем
где q есть количество продукции, z1 и z2 — количество затраченных факторов производства, a и b — определяемые технологией постоянные величины.
Пример применения
Предположим, что есть два фактора производства, «шины» и «рули». Фирма производит четырёхколёсные автомобили. В приведённой выше формуле величина q будет соответствовать количеству выпущенных машин, z1 и z2 — количеству использованных в производстве шин и рулей соответственно. Тогда функция Леонтьева принимает вид
- Количество машин= Min{¼ от количества шин, 1 от количества рулей}.
Производственная функция
Функция Леонтьева используется в качестве производственной функции в модели Харрода — Домара[1][2]:
- ,
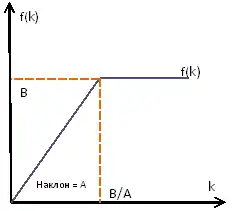
Р. Барро и Х. Сала-и-Мартин отмечают, что производственная функция Леонтьева (функция с фиксированными пропорциями) является частным случаем CES-функции[3]:
- в случае когда она принимает вид функции Леонтьева:
- ,
- где и — константы.
Таким образом, при — все работники и машины загружены; при — капитал используется в объёме , а оставшийся не востребован; при — объём труда используется в объеме , а остальной остается безработным. Допущение об отсутствии взаимозаменяемости между капиталом и трудом приводит к тому, что существует или бесконечный рост безработицы или простой оборудования.
При подушевом рассмотрении производственная функция имеет вид[3]:
- ,
- где , .
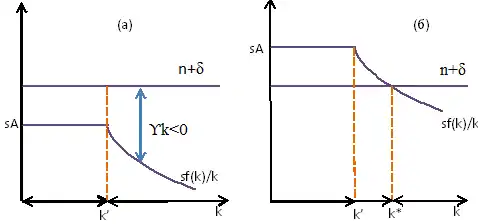
При капитал полностью используется и , и кривая производственной функции пересекает ноль и имеет наклон .
При капитал постоянен и , . При предельный продукт , а значит условие Инады выполнено, производственная функция не генерирует эндогенный рост.
При форма кривой сбережения — прямая на уровне , а при кривая сбережения стремится к нулю при .
Кривая амортизация имеет форму горизонтальной прямой на уровне .
При низкой ставке сбережения кривая сбережения не пересекает кривую амортизации, так что стационарного состояния нет, темп прироста капитала отрицателен, экономика сжимается , в ней постоянно растущая безработица.
При высокой ставке сбережения кривая сбережения приближается к нулю при и пересекает кривую амортизации в точке устойчивого стационарного значения , так что темп прироста капитала отрицателен при , а при положителен. При простаивает оборудование, часть капитала не востребована и монотонно возрастает, но при этом нет незанятых работников. Так как — константа в стационарном состоянии, то темп роста равен темпу роста и равен . Доля используемого оборудования постоянна, количество невостребованного оборудования растет с темпом . Стационарное состояние, в котором капитал и труд полностью востребованы в производстве, [3].
См. также
Примечания
- Solow, 1956.
- Нуреев, 2008, с. 26—29.
- Барро, Сала-и-Мартин, 2010, с. 97—100.
Литература
- Solow R. M. A Contribution to the Theory of Economic Growth // The Quarterly Journal of Economics. — 1956. — Февраль (vol. 70, № 1). — P. 65—94.
- Allen R. G. D. Macro-economic Theory: A Mathematical Treatment (англ.). — London: Macmillan, 1968. — P. 35.
- Барро Р. Д., Сала-и-Мартин Х. Экономический рост / Пер. с англ.. — М.: Бином. Лаборатория знаний, 2010. — 824 с. — ISBN 978-5-94774-790-4.
- Нуреев Р. М. Экономика развития: модели становления рыночной экономики. — М.: НОРМА, 2008. — 367 с. — ISBN 978-5-468-00159-2.