Функция Дикмана
В аналитической теории чисел функцией Дикмана (другое название — функция Дикмана — де Брёйна) ρ называется специальная функция, используемая для оценки числа гладких чисел для заданной границы. Впервые функция появилась у Карла Дикмана, в его единственной статье, посвященной математике[1]. Позже функция была изучена датским математиком Николасом де Брёйном[2][3].
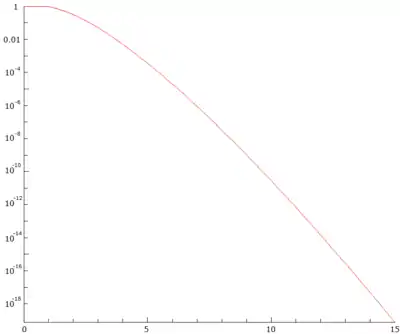
Определение
Функция Дикмана — де Брёйна — это непрерывная функция, удовлетворяющая дифференциальному уравнению со сдвигом
с начальными условиями для 0 ≤ u ≤ 1.
Дикман, основываясь на эвристических соображениях, показал, что
где — число y-гладких целых, меньших x.
В. Рамасвами (V. Ramaswami) позднее дал строгое доказательство, что
Приложения
Основное приложение функция Дикмана-де Брёйна находит в оценке частоты появления гладких целых в заданных границах. Функция может быть использована для оптимизации различных теоретико-числовых алгоритмов, хотя и сама по себе она интересна.
Используя , можно показать, что [5]
- ,
что связано с оценкой , приведенной ниже.
Постоянная Голомба — Дикмана имеет альтернативное определение в терминах функции Дикмана — де Брёйна.
Оценка
Простым приближением может служить Лучшую оценку даёт[6]
- ,
где Ei — интегральная показательная функция, а ξ — положительный корень уравнения
Простую верхнюю оценку дает
| 1 | 1 |
| 2 | 3.0685282⋅10-1 |
| 3 | 4.8608388⋅10-2 |
| 4 | 4.9109256⋅10-3 |
| 5 | 3.5472470⋅10-4 |
| 6 | 1.9649696⋅10-5 |
| 7 | 8.7456700⋅10-7 |
| 8 | 3.2320693⋅10-8 |
| 9 | 1.0162483⋅10-9 |
| 10 | 2.7701718⋅10-11 |
Вычисление
Для каждого интервала [n − 1, n] с целым n существует аналитическая функция , такая, что . Для 0 ≤ u ≤ 1, . Для 1 ≤ u ≤ 2, . Для 2 ≤ u ≤ 3,
- ,
где Li2 — дилогарифм. Остальные могут быть вычислены, используя бесконечные ряды[7].
Альтернативным методом вычисления может служить определение верхней и нижней границ методом трапеций[6][8].
Расширение
Бах и Перальта определили двумерный аналог функции [7]. Эта функция используется для оценки функции , аналогичной функции де Брёйна, но учитывающей число y-гладких целых чисел с хотя бы одним простым множителем, большим z. Тогда
Ссылки
- Dickman, K. On the frequency of numbers containing prime factors of a certain relative magnitude (англ.) // Arkiv för Matematik, Astronomi och Fysik : journal. — 1930. — Vol. 22A, no. 10. — P. 1—14.
- de Bruijn, N. G. On the number of positive integers ≤ x and free of prime factors > y (англ.) // Indagationes Mathematicae : journal. — 1951. — Vol. 13. — P. 50—60.
- de Bruijn, N. G. On the number of positive integers ≤ x and free of prime factors > y, II (англ.) // Indagationes Mathematicae : journal. — 1966. — Vol. 28. — P. 239—247.
- Ramaswami, V. On the number of positive integers less than and free of prime divisors greater than xc (англ.) // Bulletin of the American Mathematical Society : journal. — 1949. — Vol. 55. — P. 1122—1127.
- Hildebrand, A.; Tenenbaum, G. Integers without large prime factors (неопр.) // Journal de théorie des nombres de Bordeaux. — 1993. — Т. 5, № 2. — С. 411—484.
- van de Lune, J.; Wattel, E. On the Numerical Solution of a Differential-Difference Equation Arising in Analytic Number Theory (англ.) // Mathematics of Computation : journal. — 1969. — Vol. 23, no. 106. — P. 417—421. — doi:10.1090/S0025-5718-1969-0247789-3.
- Bach, Eric; Peralta, René. Asymptotic Semismoothness Probabilities (англ.) // Mathematics of Computation : journal. — 1996. — Vol. 65, no. 216. — P. 1701—1715. — doi:10.1090/S0025-5718-96-00775-2.
- Marsaglia, George; Zaman, Arif; Marsaglia, John C. W. Numerical Solution of Some Classical Differential-Difference Equations (англ.) // Mathematics of Computation : journal. — 1989. — Vol. 53, no. 187. — P. 191—201. — doi:10.1090/S0025-5718-1989-0969490-3.