Теорема о бабочке
Теорема о бабочке — классическая теорема планиметрии.
История
Опубликована в 1803 году Уильямом Уоллесом в английском журнале «The Gentlemen's Mathematical Companion». Позднее еще не раз переоткрывалась.
Формулировка
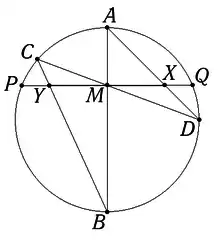
Пусть через точку М, являющуюся серединой хорды PQ некоторой окружности, проведены две произвольные хорды АВ и CD той же окружности. Пусть хорды AD и ВС пересекают хорду PQ в точках X и Y. Тогда М является серединой отрезка XY.
Замечания
Верна и обратная теорема о бабочке:
- Пусть через точку М внутри некоторой окружности проведены две произвольные хорды АВ и CD. Пусть хорды AD и ВС пересекают произвольную хорду PQ в точках X и Y. Тогда если М является серединой отрезка XY, то она одновременно является серединой хорды PQ.
О доказательствах

Доказательство
Теорема о бабочке имеет большое число различных доказательств, как в рамках элементарной геометрии, так и использующих методы, выходящие за её пределы.
- В частности, в проективной модели плоскости Лобачевского, треугольник центрально симметричен и отсюда легко следует теорема.
- При помощи проецирования двойных отношений: Рассмотрим двойное отношение точек , и спроецируем его на окружность из точки . Точки и перейдут сами в себя, так как принадлежат окружности, а точки и перейдут в точки и соответственно. Получаем (последнее следует трактовать как двойное отношение точек на комплексной плоскости). Проецируем обратно на прямую с центром в точке , получаем . Распишем двойное отношение по определению, получим необходимое равенство.
- Используется также метод инверсии[1]
Вариации и обобщения
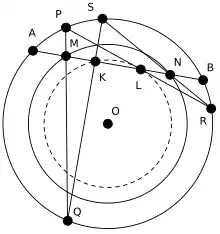
Обобщение Шарыгина.
Ссылки
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Ченцов Н. Н., Шклярский Д. О., Яглом И. М. Избранные задачи и теоремы элементарной математики. Геометрия (планиметрия). — М.: Гостехиздат, 1952.
- Жижилкин И. Д. Инверсия.. — М.: МЦНМО, 2009. — С. 36.
Примечания
- Жижилкин И. Д. Инверсия.. — М.: МЦНМО, 2009.
- Протасов В. Ю., Тихомиров В. М. Геометрические шедевры И. Ф. Шарыгина. В книге «Геометрические олимпиады имени И. Ф. Шарыгина», стр. 146.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.