Теорема Тевенена

Для линейных электрических цепей теорема утверждает, что любая электрическая цепь, имеющая два вывода и состоящая из произвольной комбинации источников напряжения, источников тока и резисторов (сопротивлений), электрически для этих двух выводов эквивалентна цепи с одним идеальным источником напряжения с ЭДС ${\displaystyle V}$ и одним резистором ${\displaystyle R}$, соединёнными последовательно с этим источником напряжения.

Иначе говоря, ток в любом сопротивлении ${\displaystyle Z_{n}}$, присоединенном к любой цепи, равен току в этом же сопротивлении ${\displaystyle Z_{n}}$, присоединённом к идеальному источнику напряжения с напряжением, равным напряжению холостого хода цепи (напряжению на этих зажимах когда к ним ничего не подключено) и обладающим внутренним сопротивлением ${\displaystyle Z_{i}}$, равным полному сопротивлению «закрытой части» цепи, определённому со стороны зажимов ${\displaystyle Z_{n}}$ при условии, что все источники внутри цепи заменены полными сопротивлениями, равными внутренним полным сопротивлениям этих источников.

То есть, экспериментально, параметры эквивалентной замены «чёрного ящика» с двумя выводами определяются из двух измерений — опыта холостого хода и опыта короткого замыкания. Пусть напряжение на зажимах (выводах) при холостом ходе будет ${\displaystyle V,}$ а ток при коротком замыкании этих же зажимов ${\displaystyle I,}$ тогда:

${\displaystyle V_{th}=V}$ и ${\displaystyle R_{th}=V/I}$

где ${\displaystyle V_{th}}$ — ЭДС идеального источника напряжения в эквивалентной замене,

${\displaystyle R_{th}}$ — сопротивление последовательно включенного с источником резистора в эквивалентной замене.

Если известна структура и параметры некоторой цепи, то формально можно вычислить параметры эквивалентной замены. При этом анализе при вычислении эквивалентного сопротивления все идеальные источники напряжения, входящие в цепь, мысленно закорачиваются, и вычисляется сопротивление полученной цепи относительно рассматриваемых зажимов. Далее пользуясь, например, правилами Кирхгофа вычисляется напряжение на зажимах. Полученные сопротивление и напряжение как раз и будут параметрами эквивалентной замены.

Теорема также применима для цепей синусоидального переменного тока в установившемся режиме, но при этом учитываются не активные сопротивления, токи и напряжения, а соответственно импедансы и комплексные амплитуды токов и напряжений.

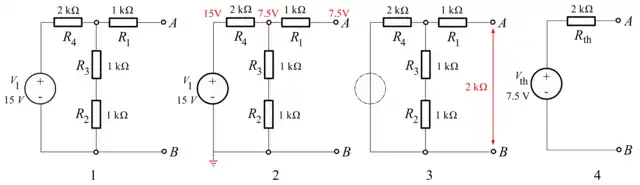
1. Исходная электрическая цепь
2. Вычисление эквивалентной ЭДС
3. Вычисление сопротивления эквивалентного резистора — источник напряжения мысленно закорочен
4. Результат эквивалентной замены

Вычисление эквивалентного напряжения (ЭДС) — напряжение, снимаемое с резистивного делителя напряжения состоящего из сопротивлений ${\displaystyle R_{4},R_{3},R_{2}}$, так как рассчитывается режим холостого хода, ток через резистор ${\displaystyle R_{1}=0}$ и падение напряжения на нём нулевое:

${\displaystyle V_{\mathrm {Th} }={R_{2}+R_{3} \over (R_{2}+R_{3})+R_{4}}\cdot V_{\mathrm {1} }=}$

${\displaystyle ={1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \over (1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )+2\,\mathrm {k} \Omega }\cdot 15\,\mathrm {V} =}$

${\displaystyle ={1 \over 2}\cdot 15\,\mathrm {V} =7.5\,\mathrm {V} .}$

Вычисление эквивалентного сопротивления, источник напряжения закорочен:

${\displaystyle R_{\mathrm {Th} }=R_{1}+\left[\left(R_{2}+R_{3}\right)\|R_{4}\right]=}$

${\displaystyle =1\,\mathrm {k} \Omega +\left[\left(1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \right)\|2\,\mathrm {k} \Omega \right]=}$

${\displaystyle =1\,\mathrm {k} \Omega +\left({1 \over (1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )}+{1 \over (2\,\mathrm {k} \Omega )}\right)^{-1}=2\,\mathrm {k} \Omega .}$

Здесь символом ${\displaystyle \|}$ обозначено сопротивление параллельного соединения резисторов ${\displaystyle R_{4}}$ и ${\displaystyle R_{2}+R_{3}.}$

• Метод эквивалентного генератора
• Теорема компенсации
• Законы Кирхгофа

• Пейдж Ч. Алгебра электроники. — М.: Госэнерго, 1962. — 351 с.