Судоку
Судо́ку (яп. 数独 су:доку, произношение ) — головоломка с числами. Иногда судоку называют магическим квадратом, что в общем-то неверно, так как судоку является латинским квадратом 9-го порядка. Судоку активно публикуют газеты и журналы разных стран мира, сборники судоку издаются большими тиражами. Решение судоку — популярный вид досуга.
Правила
Игровое поле представляет собой квадрат размером 9×9, разделённый на меньшие квадраты со стороной в 3 клетки. Таким образом, всё игровое поле состоит из 81 клетки. В них уже в начале игры стоят некоторые числа (от 1 до 9), называемые подсказками. От игрока требуется заполнить свободные клетки цифрами от 1 до 9 так, чтобы в каждой строке, в каждом столбце и в каждом малом квадрате 3×3 каждая цифра встречалась бы только один раз.
Сложность судоку зависит от количества изначально заполненных клеток и от методов, которые нужно применять для её решения. Самые простые решаются дедуктивно: всегда есть хотя бы одна клетка, куда подходит только одно число. Некоторые головоломки можно решить за несколько минут, на другие можно потратить часы.
Правильно составленная головоломка имеет только одно решение. Тем не менее, на некоторых сайтах в интернете под видом усложнённых головоломок пользователю предлагаются варианты судоку с несколькими вариантами решения, а также с ветвлениями самого хода решения.
Происхождение
В XVIII веке Леонард Эйлер изобрёл игру «Carré latin» («Латинский квадрат»). На основе этой игры в 1970-х годах в Северной Америке были придуманы специальные числовые головоломки. Так, в США судоку появилась впервые в 1979 году в журнале «Dell Puzzle Magazine». Тогда она называлась «Number Place». Настоящую популярность судоку завоевала в 1980—1990-х годах, когда японский журнал «Nikoli» начал регулярно публиковать на своих страницах эту головоломку (с 1986 года). Сегодня судоку — обязательный компонент многих газет. Среди них много изданий с многомиллионными тиражами, например, немецкая газета «Die Zeit»[1], австрийский «Der Standard»[2]. В России судоку также публикуются в десятках[уточнить] газет, журналов и в специализированных сборниках.
Математическая основа
Задача обобщённого судоку на поле является NP-полной, так как к ней сводится задача о заполнении латинского квадрата[3].
Количество различных судоку классического размера 9×9 с однозначным решением равно
или примерно . Если, однако, считать одинаковыми те судоку, которые получаются друг из друга с помощью поворотов, отражений и перенумерации, то это количество уменьшается до 5 472 730 538 (последовательность A109741 в OEIS[4],
Долгое время оставался открытым вопрос о минимальном количестве подсказок, необходимых для однозначного решения судоку. В частности, не было известно, существует ли однозначно решаемая судоку с 16 подсказками. Проект распределённых вычислений Sudoku@vtaiwan на платформе BOINC занимался поиском такой судоку[5]. В январе 2012 года появилось доказательство того, что однозначно решаемых судоку с 16 подсказками не существует[6].
Методы поиска решения
Лучший метод решения — записывать числа-кандидаты в вершине левого угла ячейки, а затем вычёркивать невозможные по правилам игры числа из данной ячейки. После этого можно увидеть именно те числа, которые могут занимать данную ячейку. Играть в судоку рекомендуется медленно, так как это расслабляющая игра.
Сначала смотрят на ряды, столбцы и блоки 3×3 с наиболее заполненными квадратами: легче решить там, где вариантов меньше. При заполнении ячейки нужно проверить столбец, ряд и блок 3×3. Нужно проверить, что все другие 8 чисел не дублируются.
Когда в судоку осталось несколько открытых ячеек в блоке 3×3 и только одна ячейка подходит для данного числа, то именно это число нужно записать в данную ячейку. Перед заполнением следует удостовериться, что вписываемое в ячейку число не будет встречаться в другой ячейке в том же столбце, строке или в блоке 3×3.
Когда в одном столбце, строке, или блоке 3×3 три любых ячейки имеют числа-кандидаты {1,2; 1,2; 1,3}, то число для третьей ячейки должно быть 3. Потому что, если бы это было число 1, то в одной из первых двух ячеек было бы число 2, а в другой не было бы ничего, но такого быть не может, поскольку все клетки должны быть заполнены.
Имеются две стратегии, используемые для увеличения скорости решения головоломки.
Выбрать число, которое было найдено для большинства строк, столбцов или блоков 3×3 в судоку. Для каждого блока 3×3, который не содержит это число, ищутся другие блоки 3×3 в том же самом ряду и столбце блоков 3×3, которые содержат это «наиболее решённое число» и в решаемом блоке, исключаются места, где это число, не может быть вписано в ячейку. Таким образом найдётся единственная ячейка для этого числа.
Пример:
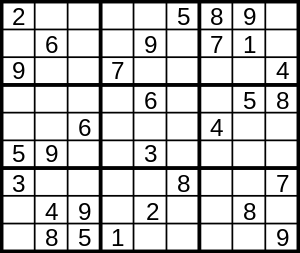
Число 9 встречается 6 раз в шести блоках 3×3. Таким образом, число 9 можно смело ставить в центральном нижнем блоке 3×3 в верхнем левом углу, а также в центральном правом блоке 3×3 в первой ячейке первого ряда. В центральном блоке 3×3 число 9 может стоять только в третьей ячейке второго ряда.
Пример:
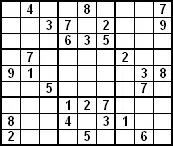
Середина верхнего ряда блоков 3×3 и середина нижнего ряда блоков 3×3 почти полностью заполнены. В середине верхнего блока три нерешённых числа — 1, 4, и 9. Анализируя такую ситуацию, можно вписать число 4 в центр блока, число 1 в правый верхний угол, а число 9 — в левый верхний угол. Аналогично можно поступить с нижним центральным блоком 3×3: в нём отсутствуют числа 6, 8 и 9. Ячейки заполняются последовательно: число 6 ставим в центр, число 9 в нижний правый угол, а число 8 в нижний левый угол.
Наиболее сложные судоку можно решать методом исключения («нить Ариадны»), для этого на отдельном листе в клеточку записывается текущее положение дел, выбирается поле, в котором могут стоять только два числа, при подстановке которых определяется как можно большее число пар в других клетках. Выбирается одно из чисел пары и подставляется в черновик. С вероятностью 50 % решение заведёт в тупик — что означает, что выбранное число было неправильным. В таком случае нужно «смотать нить» — вернуться к «развилке» и выбрать и подставить другое число. Если не было допущено ошибок в решении, подставленное число будет единственным верным. Подобный подход подробно описал Cleve Moler, создатель пакета для научных расчётов MATLAB[7].
Разновидности
Существует множество вариаций судоку:
- Нерегулярное судоку (их ещё называют Судоку-пазл, Судоку-фигуры, Области). В этой головоломке вместо стандартных областей 3×3 используются области произвольной формы. Цифры не должны повторяться в каждой такой области.
- Судоку разных размеров. Встречаются судоку размером от 4×4 (такие уменьшенные головоломки называют «шидоку» (Shidoku) от японского shi — четыре[7]) до 25×25. Наиболее распространены судоку небольших размеров для детей.
- Судоку с дополнительными областями. В этих задачах помимо стандартных областей (вертикалей, горизонталей и блоков) задаются дополнительные области, в которых цифры не могут повторяться. Наиболее распространены диагональные судоку.
- Судоку с дополнительными условиями. В таких задачах помимо стандартного условия неповторяемости цифр задаются ещё дополнительные условия на значения. Например:
- Судоку «Суммы» и множество её вариаций («Судоку-Произведения», «Судоку-Арифметика», «Квадросудоку», «Суммы-сбоку», «Суммы по диагонали» и т. п.), где всё поле делится на блоки, для которых сообщается сумма (произведение, разность и т. п.) всех входящих в него цифр.
- Судоку «Чёт-нечёт». В них некоторые клетки изначально выделены цветом, в этих клетках находятся или только чётные, или только нечётные цифры.
- Судоку «Больше-меньше». Для некоторых соседних клеток указан знак, показывающий в какой из клеток цифра больше.
- Судоку «Точки», где между соседними клетками выводится точка белого или чёрного цвета, когда соседние цифры отличаются на 1 или в два раза.
- Судоку «Перегородки» («Судоку-Соседи»), где отмечены все места с цифрами в соседних клетках отличающихся на 1.
- «Шахматные» судоку, где две или более клеток, которые связаны между собой ходом определённой шахматной фигуры (чаще всего коня), не могут содержать одинаковые цифры. Данное ограничение может налагаться на все возможные цифры или на некоторые из них.
- Судоку другой формы. В головоломке используется не квадратная сетка, а треугольная, шестиугольная или более хитроумной формы.
- Сцепленные судоку. «Судоку-Самурай» («Судоку-Комбо», «Судоку-Конструкции», «Тудоку» и др.), в которых несколько отдельных судоку имеют общие блоки и решаются взаимозависимо.
Настольная игра судоку
Существуют также настольные варианты игры. Подобные игры были изданы по всему миру различными издателями и разработчиками (к примеру, известный разработчик настольных игр Reiner Knizia издал свой вариант этой логической игры). В России можно встретить настольные судоку от фирмы Астрель и польской компании Trefi[8].
Компьютерные игры
Для персональных компьютеров существует достаточно много вариантов данной игры, например,
- Sudoku (из набора игр GNOME Games) или KSudoku (из набора игр KDE Games) — для Linux-платформ,
- Microsoft Sudoku (доступная для ОС Windows 8.1 или Windows 10 в Windows Store) — для Windows-платформ.
Версии для мобильных телефонов
Существуют несколько версий игры для мобильных телефонов, а также для смартфонов. Эти версии удобны тем, что могут сами создавать условие головоломки. Также они указывают на ошибки (противоречащие цифры подсвечиваются) или могут дать подсказку в решении. 9 цифр в стандартных судоку, назначенные на 9 цифровых кнопок на мобильном телефоне, делают процесс игры очень удобным.
С появлением смартфонов игра заняла достойное место среди самых популярных. С выходом на рынок устройств на базе Android и iOS, количество поклонников игры резко возросло.
См. также
Примечания
- Die Zeit Архивная копия от 12 сентября 2005 на Wayback Machine (нем.)
- Der Standard ›Lifestyle›Spielen & Lesen›Spielen›Sudoku (нем.)
- T. Yato, T. Seta. Complexity and Completeness of Finding Another Solution and Its Application to Puzzles Архивная копия от 21 июля 2011 на Wayback Machine (англ.).
- Jarvis, Frazer; Russell, Ed. There are 5472730538 essentially different Sudoku grids ... and the Sudoku symmetry group. Frazer Jarvis's home page (7 сентября 2005). Дата обращения: 16 сентября 2006.
- Sudoku@vtaiwan — Проект распределённых вычислений по исследованию судоку Архивировано 19 августа 2013 года.
- Математики решили задачу о подсказках в судоку
- Cleve Moler. Solving Sudoku with MATLAB.
- Судоку — тренировка для ума Архивная копия от 14 июня 2007 на Wayback Machine (недоступная ссылка с 13-05-2013 [3213 дней] — история).
Литература
- Эндрю Херон, Эдмунд Джеймс. Судоку для «чайников» = Su Doku for Dummies (Sudoku). — М.: «Диалектика», 2007. — С. 336. — ISBN 978-0-470-01892-7.
- К. Кноп. Магический квадрат или Числа на плацу // Компьютерра. — Вып. 09.09.2000.
- И. Г. Сухин. Судоку и суперсудоку на шестнадцати клетках для детей. — М.: АСТ, Астрель, 2006. — 128 с. — ISBN 5-17-036566-7.
