Собственное ускорение
Собственное ускорение[1] в теории относительности — физическое ускорение (то есть измеримое ускорение, например помощью акселерометра), испытываемое объектом. Таким образом, это ускорение относительно свободного падения или инерциального наблюдателя, который на мгновение находится в состоянии покоя относительно измеряемого объекта. Гравитация не вызывает собственного ускорения, так как гравитация воздействует на инерциального наблюдателя таким образом, что собственное ускорение не фиксируется. Следствием является то, что все инерционные наблюдатели всегда имеют нулевое собственное ускорение.
Собственное ускорение контрастирует с ускорением, которое зависит от выбора системы координат и, следовательно, от выбора наблюдателя.
В стандартных инерциальных координатах специальной теории относительности для однонаправленного движения собственным ускорением является скорость изменения собственной скорости относительно координатного времени.
В инерциальной системе, в которой объект мгновенно находится в состоянии покоя, собственный 3-вектор ускорения, объединённый с нулевой временной компонентой, дает 4-ускорение объекта, что делает величину собственного ускорения лоренц-инвариантной. Таким образом, концепция полезна в следующих случаях: (i) с ускоренными системами координат, (ii) на релятивистских скоростях и (iii) в искривленном пространстве-времени.
В ускоряющей ракете после запуска или даже в ракете, стоящей на старте, собственное ускорение — это ускорение, ощущаемое обитателями, и которое описывается как перегрузка (что не является силой, а является именно ускорением, см. эту статью для более подробного обсуждения собственного ускорения), производимой только транспортными средствами.[2] «Ускорение гравитации» («сила тяжести») никогда не делает вклад в собственное ускорение ни при каких обстоятельствах, а значит собственное ускорение, наблюдаемое наблюдателями, стоящими на земле, обусловлено механической силой из земли, а не из-за «силы» или «ускорения» силы тяжести. Если убрать землю и позволить наблюдателю свободно падать, наблюдатель испытает координатное ускорение, но не будет собственного ускорения и, следовательно, не будет перегрузки. Обычно объекты в таком падении или вообще при любом баллистическом пути (также называемом инерциальным движением), в том числе объекты на орбите, не испытывают собственного ускорения (пренебрегая небольшими приливными ускорениями для инерциальных путей в гравитационных полях). Это состояние также известно как «невесомость» («ноль-g») или «свободное падение».
Собственное ускорение сводится к координатному в инерциальной системе координат в плоском пространстве-времени (то есть при отсутствии силы тяжести), при условии, что величина собственной скорости объекта[3] (импульс на единицу массы) намного меньше скорость света c. Только в таких ситуациях координатное ускорение полностью ощущается как перегрузка (то есть собственное ускорение, также определяемое как создающее измеримый вес).
В ситуациях, когда гравитация отсутствует, но выбранная система координат не является инерциальной, а ускоряется с наблюдателем (например, ускоренной системой отсчета ускоряющей ракеты или рамкой, закрепленной на объектах в центрифуге), то перегрузки и соответствующие собственные ускорения, наблюдаемые наблюдателями в этих системах координат, вызваны механическими силами, которые сопротивляются их весам в таких системах. Этот вес, в свою очередь, создается силами инерции, которые появляются во всех таких ускоренных системах координат, подобно весу, создаваемому «силой гравитации» для объектов, зафиксированных в пространстве относительно гравитирующего тела (как на поверхности Земли).
Суммарная (механическая) сила, которая рассчитывается, чтобы вызвать собственное ускорение покоящейся массы в системе координат, которая имеет собственное ускорение, по закону Ньютона F = m a, называется собственной силой. Как видно выше, собственная сила равна силе противодействия, которая измеряется как «рабочий вес» объекта (то есть его вес, измеренный устройством, подобным пружинным весам, в вакууме, в системе координат объекта). Таким образом, собственная сила объекта всегда численно равна и противоположна по направлению измеренному весу.
Примеры
При удержании на карусели, которая вращается с постоянной угловой скоростью, вы испытываете радиальное внутреннее (центростремительное) собственное ускорение из-за взаимодействия между рукояткой и рукой. Это отменяет радиально внешнее геометрическое ускорение, связанное с вращающейся системой отсчета. Это внешнее ускорение (с точки зрения вращающейся системы отсчета) станет координатным ускорением, когда вы отпустите руки, что приведет к полету по геодезической с нулевым собственным ускорением. Разумеется в этот момент неускоренные наблюдатели в своей системе отсчета просто видят, как исчезают ваши равные собственные и координатные ускорения.
Анимация: отпускание рук на карусели 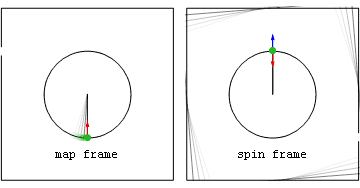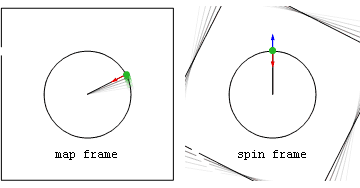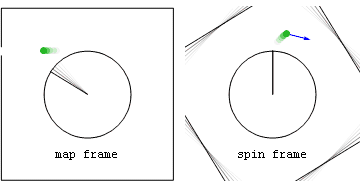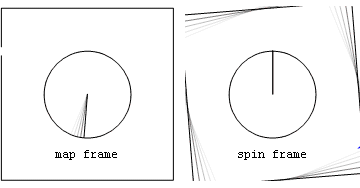 Вид из покоящейся (слева) и вращающейся (справа) систем отсчета собственного (красный) и геометрического (синих) ускорений для объекта, выпущенного с карусели.
Вид из покоящейся (слева) и вращающейся (справа) систем отсчета собственного (красный) и геометрического (синих) ускорений для объекта, выпущенного с карусели.С точки зрения покоящейся системы отсчета, опасна тангенциальная скорость. С точки зрения вращающейся системы отсчета опасность может исходить от геометрического ускорения. Примечание: В некоторых браузерах вы можете нажать [Esc], чтобы остановить движение для более детального изучения. Однако вам может потребоваться перезагрузить страницу для повторного старта анимации.
Точно так же, стоя на невращающейся планете (и на земле), мы испытываем собственное ускорение вверх из-за нормальной (перпендикулярной поверхности) силы, создаваемой землей на подошву нашей обуви. Она нейтрализует геометрическое ускорение в нижнем направлении из-за выбора системы координат (так называемая система отсчета поверхности (англ. shell frame)[4]). Это ускорение вниз становится координатным, если мы случайно шагнем с обрыва в траекторию нулевого собственного ускорения (геодезическая или система отсчета дождя).
Анимация: мяч, который скатывается со скалы 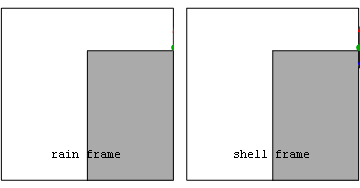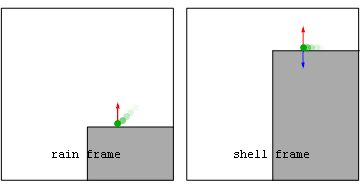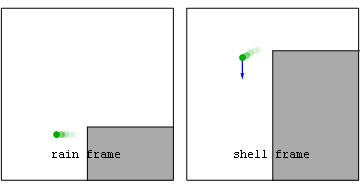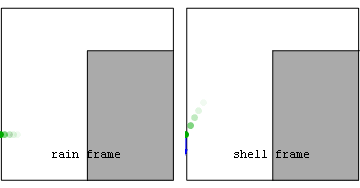 Изображения в системе отсчета дождя (rain frame) и поверхности (shell frame) собственного (красное) и геометрического (синее) ускорения для объекта, который скатывается со скалы.
Изображения в системе отсчета дождя (rain frame) и поверхности (shell frame) собственного (красное) и геометрического (синее) ускорения для объекта, который скатывается со скалы.
Обратите внимание, что геометрическое ускорения (из-за члена аффинной связности в системе координат ковариантная производной) действуют на каждый грамм нашего существа, в то время как собственные ускорения обычно вызваны внешней силой. Вводные курсы физики часто рассматривают гравитационное ускорение вниз (геометрическое) как следствие гравитационной силы. Это, наряду со старательным уклонением от неускоренных систем отсчета, позволяет им рассматривать координатное и собственное ускорения как к одну и ту же сущность.
Даже тогда, когда объект поддерживает постоянное собственное ускорение в течение длительного периода времени в плоском пространстве-времени, покоящиеся наблюдатели будут видеть, что координатное ускорение объекта уменьшается, по мере того как его координатная скорость приближается к скорости света. Тем не менее темп роста собственной скорости движения объекта остается постоянным.
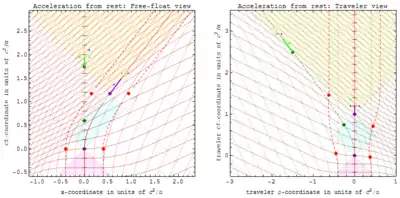
Анимация: быстрый подъём и спуск  Вид в системе отсчета покоя собственного (красное) и координатного (зеленое) ускорений/торможений в вертикальном направлении.
Вид в системе отсчета покоя собственного (красное) и координатного (зеленое) ускорений/торможений в вертикальном направлении.Здесь наш объект сначала ускоряется вверх в течение периода времени 2*c/α по часам путешественника, где c — скорость света, а α — (красная) величина собственного ускорения. Этот первый этап занимает около 2 лет, если величина ускорения составляет около 1g. Затем он ускоряется вниз (сначала замедляется, а затем ускоряется) в течение удвоенного периода, а затем замедляется 2*c/α, чтобы вернуться на исходную высоту. Обратите внимание, что координатное ускорение (зеленое) является заметным только во время низкоскоростных отрезков этого путешествия.
Таким образом, различие между собственным и координатным ускорением[5] позволяет отслеживать опыт ускоренных путешественников с различных не ньютоновских перспектив. Эти перспективы включают в себя такие случаи как ускоренные системы координат (например, карусели), высокие скорости (когда собственные и координатные времена отличаются) и искривленное пространства-время (например, связанного с гравитацией на Земле).
Классические приложения
На низких скоростях в инерциальных систем координат Ньютоновской физики собственное ускорение равно координатному ускорению a=d2x/dt2. Однако, как было сказано выше, оно отличается от координатного ускорения, если вы выбираете (против совета Ньютона) описание мира с точки зрения ускоренной системы координат, например, ускоренного автомобиля, или камня, вращающегося в рогатке. Если вы согласитесь, что гравитация вызвана кривизной пространства-времени (см. ниже), в гравитационном поле собственное ускорение отличается от координатного.
Например, объект, подвергшийся физическому или собственному ускорению ao, будет наблюдаться наблюдателями в системе координат, подвергающейся постоянному ускорению aframe с координатным ускорением:
- .
Таким образом, если объект ускоряется с системой отсчета, наблюдатели, закрепленные в этой системе отсчета, вообще не будут видеть никакого ускорения.
Анимация: поездка от блока к блоку 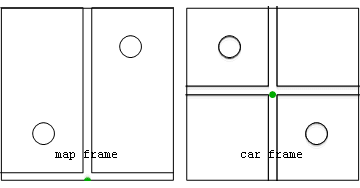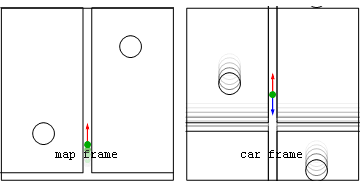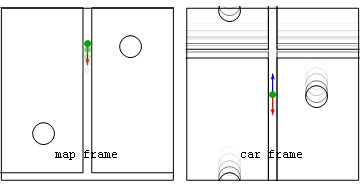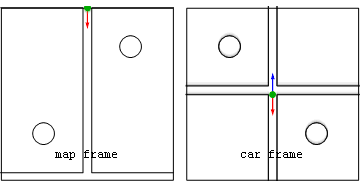 Вид из покоящейся (map frame) и автомобильной (car frame) систем отсчета физических (красные) и геометрических (синие) ускорений для автомобиля, движущегося от одного знака остановки до другого.
Вид из покоящейся (map frame) и автомобильной (car frame) систем отсчета физических (красные) и геометрических (синие) ускорений для автомобиля, движущегося от одного знака остановки до другого.На этой иллюстрации автомобиль разгоняется после знака остановки до середины блока, после чего водитель сразу же отпускает газ и нажимает на тормоз, чтобы сделать следующую остановку.
Аналогично объект, подвергающийся физическому или собственному ускорению ao, будет наблюдаться наблюдателями в системе, вращающейся с угловой скоростью ω, как имеющий координатное ускорение:
- .
В приведенном выше уравнении в правой части есть три геометрических члена ускорения. Первый — «центробежное ускорение», зависит только от радиального положения «r», а не от скорости нашего объекта, второй — «ускорение Кориолиса», зависит только от скорости объекта во вращающейся системе отсчета vrot, но не от его положения, а третий член — «ускорение Эйлера», зависит только от положения и скорости изменения угловой скорости системы отсчета.
Ньютоновский пример: рогатка с постоянной скоростью 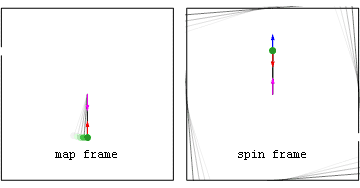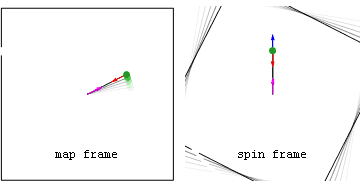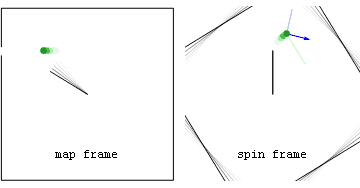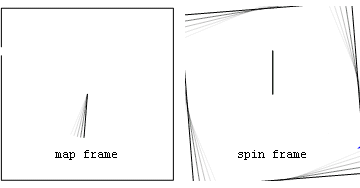 Ускорения и силы в покоящейся (map frame) и вращающейся (spin frame) системах отсчета, связанные с камнем, выпущенным после того, как его раскрутили на невесомой веревке.
Ускорения и силы в покоящейся (map frame) и вращающейся (spin frame) системах отсчета, связанные с камнем, выпущенным после того, как его раскрутили на невесомой веревке.Силы на камне включают внутреннюю центростремительную (красную) силу, наблюдаемую в обеих системах отсчета, а также геометрическую (синюю) силу, наблюдаемую во вращающейся системе отсчета. Перед тем как камень отпускают, синяя геометрическая сила является чисто центробежной (направленной радиально наружу), а после отпускания геометрическая сила представляет собой сумму центробежных и кориолисовых компонент.
Обратите внимание, что после выпуска во вращающейся системе отсчета центробежная компонента (голубая) всегда радиальная, а компонента Кориолиса (зеленая) всегда перпендикуляр к скорости вращающейся системы отсчета. Также видно, что в обоих системах сила в точке крепления веревки (пурпурная), вызванная третьим законом Ньютона, противодействует центростремительной силе на камне.
Перед запуском камня
Следующие альтернативные анализы движения до отпускания камня рассматривают только силы, действующих в радиальном направлении. Оба анализа предсказывают натяжение веревки T=mv2/r. Например, если радиус лямки равен r=1 метр, скорость камня в покоящейся системе отсчета равна v=25 метров в секунду, а масса камня m=0,2 кг, то напряжение веревки будет 125 ньютонов.
- События в покоящейся системе координат перед запуском
Здесь видно, что камень все время имеет ускорение во внутрь, чтобы перемещаться по круговой траектории радиуса r. Радиальное ускорение в радиальном направлении aradial=v2/r вызвано одной «несбалансированной» центростремительной силой T. Тот факт, что сила растяжения несбалансирован, означает, что в этой системе отсчета центробежная (радиально-наружная) сила на камне равна нулю.
- События во вращающейся системе отсчета перед запуском
С точки зрения вращающейся системы можно сказать, что камень испытывает сбалансированную внутреннюю центростремительную (T) и центробежную (mv2/r) силу, что приводит к отсутствию каких-либо ускорений с точки зрения этой системы отсчета. В отличие от центростремительной силы, зависящая от системы отсчета, центробежная сила воздействует на каждый кусочек вращающегося камня, так же как гравитация действует на каждый наш грамм. Кроме того, величина центробежной силы пропорциональна массе камня, поэтому ускорение будет независимым от массы.
После запуска камня
После того, как камень высвобождается, в вращающейся системе как центростремительные, так и кориолисовые силы действуют нелокализованно на все части камня с ускорениями, которые не зависят от массы камня. Для сравнения в покоящейся системе после высвобождения вообще никаких сил на камень не действует.
В каждом из этих случаев физическое или собственное ускорение отличается от координатного ускорения, поскольку на последнее может влиять наш выбор системы координат, а также физические силы, действующие на объект. Те компоненты координатного ускорения, которые не вызваны физическими силами (например, прямой контакт или электростатическое притяжение), часто приписываются (как в приведенном выше примере Ньютона) силам, которые: (i) действуют на каждый грамм объекта, (ii) вызывают массово-независимые ускорения и (iii) не существуют со всех точек зрения. Такие геометрические (или несобственные) силы включают в себя силы Кориолиса, силы Эйлера, перегрузку, центробежные силы и (как мы увидим ниже) силу тяжести.
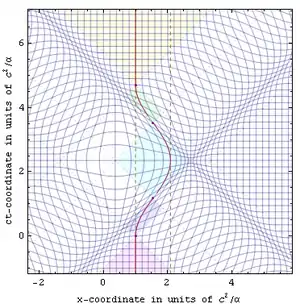
Взгляд из части плоского пространства-времени
Отношение собственного ускорения к координатному в заданной части плоского пространства-времени следует[6] из уравнения метрики плоского пространства-времени Минковского (cdτ)2 = (cdt)2 — (dx)2. Здесь единственная система отсчета из метров и синхронизированных часов определяет положение в системе покоя x и время в системе покоя t соответственно, часы движущегося объекта определяют собственное время τ, а «d» перед координатой означает бесконечно малое изменение. Эти отношения позволяют решать различные проблемы «инжиниринга любых скоростей», хотя и только с точки зрения расширенной системы отсчета покоя наблюдателя, в которой определяется одновременность.
Ускорение в (1+1)D
В однонаправленном случае, когда ускорение объекта является параллельным или антипараллельным его скорости в срединном срезе наблюдателя, правильное ускорение α и ускорение координат a связаны с[7] через Лоренц-фактор γ для α=γ3a. Следовательно, изменение собственной скорости w=dx/dτ является интегралом собственного ускорения по времени покоящейся системы t то есть Δw=αΔt для константы α. На низких скоростях это сводится к хорошо известному отношению между координатной скоростью и времени координатного ускорения, то есть Δv=aΔt.
Для постоянного однонаправленного собственного ускорения существуют аналогичные соотношения между быстротой η и прошедшим собственным временем Δτ, а также между коэффициентом Лоренца γ и пройденным расстоянием Δx. А именно:
- ,
где различные параметры скорости связаны соотношением
- .
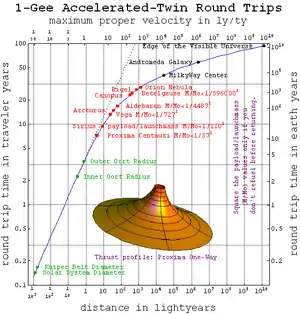
Эти уравнения описывают некоторые последствия ускоренного движения с большой скоростью. Например, представьте себе космический корабль, который может ускорять своих пассажиров в 1g (10 м/с2 или около 1.0 световых лет в год в квадрате) полпути к месту назначения, а затем тормозить их при 1g за оставшуюся половину пути, чтобы обеспечить земную искусственную гравитацию от точки A до точки B.[8][9] Для расстояний в системе покоя ΔxAB первое уравнение из приведенных выше прогнозирует средний Лоренц фактор γmid=1+α(ΔxAB/2)/c2. Следовательно, время путешествия туда и обратно по часам командира будет Δτ = 4(c/α) cosh−1(γmid), в течение которого время, прошедшее на часах системы покоя, будет Δt = 4(c/α) sinh[cosh−1(γmid)].
Этот воображаемый космический корабль мог бы предложить путешествия к Проксима Центавра и обратно, занявшие около 7.1 лет по часам путешественников (~ 12 лет по земным часам), путешествия в центральную черную дыру за около 40 лет (~ 54 000 лет, прошедших по земным часам) и путешествия в Галактику Андромеды, продолжающиеся около 57 лет (более 5 миллионов лет по земным часам). К сожалению, ускорение в 1g в течение многих лет легче сказать, чем сделать, о чём свидетельствует рисунок справа, показывающий отношение максимальной полезной нагрузки к стартовой массе.
Анимация: путешествие к звезде на расстояние 6.9 световых лет и обратно. 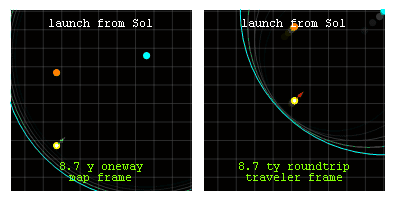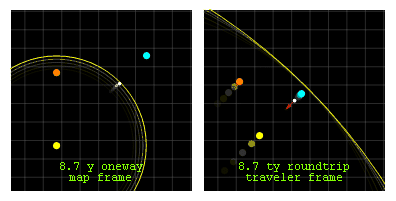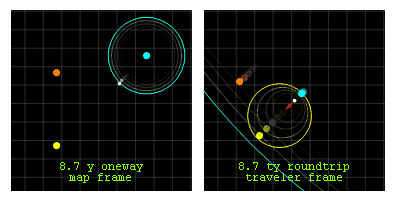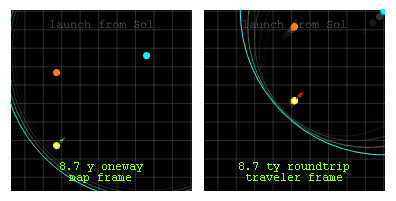 Вид из системы покоя (слева) и системы путешественника (справа) путешествия в обе стороны с постоянным ускорением 1g (красная стрелка в системе путешественника) между солнцем (желтое) и гипотетической звездой (голубая) на расстоянии в 6,9 световых лет. Проксима Центравра (оранжевый) в 4 световых годах от солнца отображается оранжевым цветом в левом верхнем углу.
Вид из системы покоя (слева) и системы путешественника (справа) путешествия в обе стороны с постоянным ускорением 1g (красная стрелка в системе путешественника) между солнцем (желтое) и гипотетической звездой (голубая) на расстоянии в 6,9 световых лет. Проксима Центравра (оранжевый) в 4 световых годах от солнца отображается оранжевым цветом в левом верхнем углу.С каждой точки зрения год должен проходить каждые две секунды или каждые 100/17,4 кадра. После каждого кругосветного полета пилоты на этом челночном рейсе будут в возрасте в два раза меньше, чем коллеги, оставшиеся на земле. Это действует замедление времени.
Другие различия включают изменения расстояния между движущимися звездами, которые видны в системе путешественника. Это действует Лоренцево_сокращение. Координатное ускорение (зеленое), наблюдаемое в системе карты, является значительным только за год до и после каждого запуска, в то время как собственное ускорение (красное), ощущаемое путешественником, значительное во время рейса.
Обратите внимание также на трассировку светового сигнала, инициированного с каждой точки запуска, но через 0.886 лет (системе карты) после запуска. Этот импульс достигает путешественника в средней точке путешествия, чтобы напоминать им о начале торможения. В системе карты Проксима Центавра видит импульс разворота до звезды назначения, но в системе путешественника верно обратное. Это относительность одновременности. Тем не менее оба наблюдателя сходятся во мнении о последовательности событий на любой времениподобной мировой линии.
Примечания
- Edwin F. Taylor & John Archibald Wheeler (1966 1st ed. only) Spacetime Physics (W.H. Freeman, San Francisco) ISBN 0-7167-0336-X, Chapter 1 Exercise 51 page 97-98: «Clock paradox III» (pdf Архивная копия от 21 июля 2017 на Wayback Machine).
- Relativity By Wolfgang Rindler pg 71
- Francis W. Sears & Robert W. Brehme (1968) Introduction to the theory of relativity (Addison-Wesley, NY) LCCN 680019344, section 7-3
- Edwin F. Taylor and John Archibald Wheeler (2000) Exploring black holes (Addison Wesley Longman, NY) ISBN 0-201-38423-X
- cf. C. W. Misner, K. S. Thorne and J. A. Wheeler (1973) Gravitation (W. H. Freeman, NY) ISBN 978-0-7167-0344-0, section 1.6
- P. Fraundorf (1996) «A one-map two-clock approach to teaching relativity in introductory physics» (arXiv: physics/9611011)
- A. John Mallinckrodt (1999) What happens when a*t>c? Архивировано 30 июня 2012 года. (AAPT Summer Meeting, San Antonio TX)
- E. Eriksen and Ø. Grøn (1990) Relativistic dynamics in uniformly accelerated reference frames with application to the clock paradox, Eur. J. Phys. 39:39-44
- C. Lagoute and E. Davoust (1995) The interstellar traveler, Am. J. Phys. 63:221-227