Относительность одновременности

Согласно специальной теории относительности Эйнштейна, невозможно сказать в абсолютном смысле, что два разных события происходят одновременно, если эти события разделены в пространстве. Если одна система отсчёта назначает одно и то же время двум событиям, находящимся в разных точках пространства, то система отсчёта, которая движется относительно первой, назначает разные времена для этих двух событий (единственное исключение — когда движение точно перпендикулярно линии, соединяющей точки этих событий).

Например, автокатастрофы в Лондоне и в Нью-Йорке являющиеся одновременными для наблюдателя на Земле, окажутся произошедшими в несколько разное время для пассажира самолёта, летящего между Лондоном и Нью-Йорком. Кроме того, если два события не могут быть причинно связаны (то есть время между событием в точке А и событием в точке В меньше времени, за которое свет проходит расстояние между А и В), то, в зависимости от состояния движения, окажется, что в одной системе отсчёта автокатастрофа в Лондоне произошла первой, а в другой системе отсчёта первой произошла автокатастрофа в Нью-Йорке. Однако, если события причинно связаны (между ними прошло больше времени, чем время прохождения света между А и В), порядок событий сохраняется во всех системах отсчёта.

В 1892 и 1895 годах Хендрик Лоренц использовал математический метод под названием «местное время» t' = t — v x/c² для объяснения экспериментов с отрицательным дрейфом эфира[1] Однако Лоренц не дал физического объяснения этого эффекта. Это было сделано Анри Пуанкаре, который ещё в 1898 году подчёркивал условную природу одновременности и утверждал, что удобно постулировать постоянство скорости света во всех направлениях. Однако эта статья не содержит обсуждения теории Лоренца или возможной разницы в определении одновременности для наблюдателей в разных состояниях движения[2][3]. Это было сделано в 1900 году, когда Пуанкаре вывел местное время, предположив, что скорость света неизменна в эфире. Из-за «принципа относительного движения» движущиеся наблюдатели в эфире также предполагают, что они находятся в состоянии покоя и что скорость света постоянна во всех направлениях (только до первого порядка по v/c). Следовательно, если они синхронизируют свои часы с помощью световых сигналов, то они будут учитывать только время прохождения сигналов, но не их движение относительно эфира. Таким образом, движущиеся часы не синхронны и не показывают «истинное» время. Пуанкаре подсчитал, что эта ошибка синхронизации соответствует местному времени Лоренца[4][5]. В 1904 году Пуанкаре подчеркнул связь между принципом относительности, «местным временем» и инвариантностью скорости света; однако рассуждения в этой статье были представлены в качественной и гипотетической манере[6][7].

Альберт Эйнштейн использовал аналогичный метод в 1905 году, чтобы получить преобразование времени для всех порядков по v/c, то есть полное преобразование Лоренца. Пуанкаре получил полное преобразование ранее, в 1905 году, но в статьях того же года он не упомянул свою процедуру синхронизации. Этот вывод был полностью основан на инвариантности скорости света и принципе относительности, поэтому Эйнштейн заметил, что для электродинамики движущихся тел эфир не нужен. Таким образом, разделение на «истинное» и «локальное» время Лоренца и Пуанкаре исчезает — все времена одинаково действительны, и поэтому относительность длины и времени является естественным следствием[8][9][10].

В 1908 году Герман Минковский ввёл понятие мировой линии частицы[11] в своей модели космоса, названной пространством Минковского. По мнению Минковского, наивное понятие скорости заменяется быстротой, и обычное ощущение одновременности становится зависимым от гиперболической ортогональности пространственных направлений к мировой линии, связанной с быстротой. Тогда каждая инерциальная система отсчёта имеет скорость и одновременную гиперплоскость.

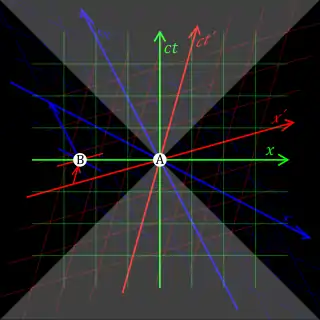
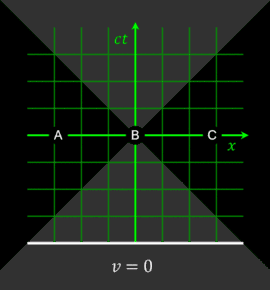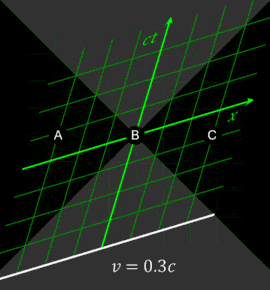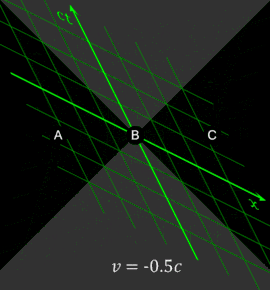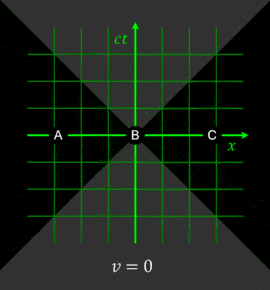
Относительность одновременности событий является ключевым эффектом СТО, проявляющимся, в частности, в «парадоксе близнецов». Рассмотрим несколько синхронизированных часов, расположенных вдоль оси ${\displaystyle \textstyle x}$ в каждой из систем отсчёта. В преобразованиях Лоренца предполагается, что в момент времени ${\displaystyle \textstyle t'=t=0}$ начала систем отсчёта совпадают: ${\displaystyle \textstyle x'=x=0}$. Ниже изображена такая синхронизация отсчёта времени (на «центральных» часах) с точки зрения системы отсчёта ${\displaystyle \textstyle S}$ (левый рисунок) и с точки зрения наблюдателей в ${\displaystyle \textstyle S'}$ (правый рисунок):

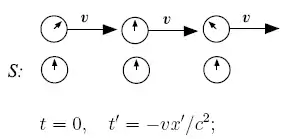
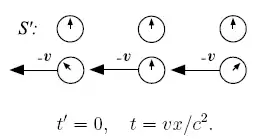
Предположим, что рядом с каждыми часами в обеих системах отсчёта находятся наблюдатели. Положив в преобразованиях Лоренца ${\displaystyle \textstyle t'=0}$, получаем ${\displaystyle \textstyle t=vx/c^{2}}$. Это означает, что наблюдатели в системе ${\displaystyle \textstyle S'}$, одновременно с совпадением времени на центральных часах, регистрируют различные показания на часах в системе ${\displaystyle \textstyle S}$. Для наблюдателей, расположенных справа от точки ${\displaystyle \textstyle x=0}$, с координатами ${\displaystyle \textstyle x>0}$, в момент времени ${\displaystyle \textstyle t'=0}$ часы неподвижной системы отсчёта показывают «будущее» время: ${\displaystyle \textstyle t=vx/c^{2}>0}$. Наблюдатели ${\displaystyle \textstyle S'}$, находящиеся слева от ${\displaystyle \textstyle x=0}$, наоборот, фиксируют «прошлое» время часов ${\displaystyle \textstyle S}$: ${\displaystyle \textstyle t<0}$. На рисунках выше положение стрелок символизирует подобную разницу показаний часов двух систем отсчёта.

Эйнштейн представлял себе неподвижного наблюдателя, который был свидетелем двух молний, одновременно попадающих в оба конца движущегося поезда. Он пришёл к выводу, что наблюдатель, стоящий на поезде, увидит, что молнии попадают в разное время.

Единое «настоящее», то есть часы, синхронно идущие в различных точках пространства, можно ввести только в рамках конкретной инерциальной системы отсчёта. Однако, этого нельзя сделать одновременно для двух различных систем отсчёта.

Движущаяся относительно неподвижных наблюдателей система с их точки зрения содержит рассинхронизированные в направлении движения часы, своеобразное непрерывное объединение «прошлого», «настоящего» и «будущего».

Эффекты замедления времени и относительности одновременности тесно связаны друг с другом и одинаково необходимы для расчёта ситуации, описанной в «парадоксе» близнецов.

Поезд и платформа

Эксперимент поезд и платформы из системы отсчёта наблюдателя в поезде

Система отсчёта наблюдателя, стоящего на платформе (Без учёта сокращения длины)

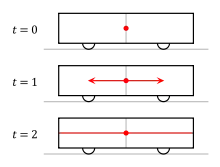
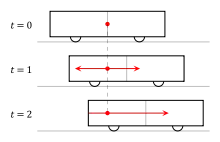
Популярная картина для понимания этой идеи обеспечивается мысленным экспериментом, подобным тому, который был предложен Комстоком в 1910 году[14] и Эйнштейном в 1917 г.[15][12] Он также состоит из одного наблюдателя в середине скоростного вагона и другого наблюдателя, стоящего на платформе, когда поезд движется мимо.

Вспышка света излучается в центре вагона в момент, когда два наблюдателя оказываются напротив друг друга. Для наблюдателя, сидящего в поезде, передняя и задняя часть вагона находятся на фиксированных расстояниях от источника света и значит, по мнению этого наблюдателя, свет достигнет передней и задней части вагона одновременно.

С другой стороны, для наблюдателя, стоящего на платформе, задняя часть вагона приближается к точке, в которой произошла вспышка, а передняя часть вагона удаляется от неё. Поскольку скорость света конечна и одинакова во всех направлениях для всех наблюдателей, свету, движущимся к задней часть поезда, нужно преодолеть меньшее расстояние, чем свету, движущимся к передней части вагона. Таким образом, вспышки света достигнут концов вагона в разное время.

Пространственно-временные диаграммы

Пространственно-временная диаграмма в системе отсчёта наблюдателя в поезде

Та же диаграмма в системе отсчёта наблюдателя, который видит движущийся вправо поезд

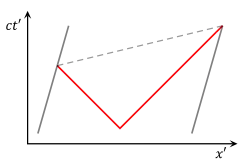
Может быть полезно визуализировать эту ситуацию, используя пространственно-временные диаграммы. Для данного наблюдателя ось t определяется как точка, продолженная вертикально во времени от начала пространственной координаты x. Ось x определяется как совокупность всех точек пространства в момент времени t=0 и продолженная горизонтально. Утверждение о том, что скорость света одинакова для всех наблюдателей, отражается путём рисования светового луча как линии под углом 45°, независимо от скорости источника относительно скорости наблюдателя.

На первой диаграмме оба конца поезда изображены серыми линиями. Поскольку концы поезда неподвижны относительно наблюдателя в поезде, эти линии являются строго вертикальными линиями, показывающими их движение во времени, но не в пространстве. Вспышка света показана в виде красных линий под углом 45°. Точки, в которых эти две световые вспышки попадают в концы поезда, находятся на диаграмме на одном уровне. Это означает, что события одновременны.

На второй диаграмме оба конца поезда, движущегося вправо, показаны параллельными линиями. Вспышка света происходит в точке ровно на полпути между двумя концами поезда и снова образует две линии под углом в 45°, выражающие постоянство скорости света. Однако на этой картине точки, на которых вспышки света попадают в концы поезда, не на одном уровне; они не одновременны.

Относительность одновременности может быть продемонстрирована с использованием преобразований Лоренца, которые связывают координаты, используемые одним наблюдателем, с координатами, используемыми другим наблюдателем, находящимся в равномерном относительном движении относительно первого.

Предположим, что первый наблюдатель использует координаты, помеченные t, x, y, z, а второй наблюдатель использует координаты, помеченные t',x',y',z'. Предположим теперь, что первый наблюдатель видит второго движущимся в направлении x со скоростью v. И предположим, что координатные оси наблюдателей параллельны и что они имеют одинаковое начало координат. Тогда преобразование Лоренца выражает взаимосвязь координат:

${\displaystyle t'={\frac {t-{v\,x/c^{2}}}{\sqrt {1-v^{2}/c^{2}}}}\ ,}$

${\displaystyle x'={\frac {x-v\,t}{\sqrt {1-v^{2}/c^{2}}}}\ ,}$

${\displaystyle y'=y\ ,}$

${\displaystyle z'=z\ ,}$

где c — скорость света. Если два события происходят одновременно в системе отсчёта первого наблюдателя, они будут иметь одинаковые значения координаты t. Однако, если они имеют разные значения координаты x (разные позиции в направлении x), то они будут иметь разные значения координаты t, и поэтому в этой системе отсчёта они будут происходить в разное время. Параметр, который учитывает нарушение абсолютной одновременности — это v x/c².

Пространственно-временная диаграмма, показывающая множество точек, рассматриваемых как одновременные неподвижным наблюдателем (горизонтальная пунктирная линия) и множество точек, рассматриваемых как одновременные наблюдателем, движущимся при v = 0,5c (пунктирная линия)

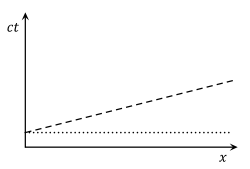
Уравнение t' = constant определяет «линию одновременности» в системе координат (x', t' ) для второго (движущегося) наблюдателя, так же как уравнение t= constant определяет «линию одновременности» для первого (стационарного) наблюдателя в системе координат (x, t ). Из приведённых выше уравнений преобразования Лоренца видно, что t' является постоянным тогда и только тогда, когда t — v x/c² = constant. Таким образом, множество точек с постоянным t, отличаются от множества точек с постоянным t' . То есть набор событий, которые рассматриваются как одновременные, зависит от системы отсчёта, используемой для их сравнения.

Графически это можно представить на пространственно-временной диаграмме тем фактом, что график множества точек, рассматриваемых как одновременные, образует линию, которая зависит от наблюдателя. В пространственно-временной диаграмме пунктирная линия представляет собой набор точек, считающихся одновременными с началом координат, наблюдателем, движущимся со скоростью v равной четверти скорости света. Пунктирная горизонтальная линия представляет собой набор точек, рассматриваемых как одновременные с началом координат стационарного наблюдателя. Эта диаграмма рисуется с использованием координат неподвижного наблюдателя (x, t ) и отмасштабирована так, что скорость света равна единице, то есть луч света будет представлен линией в 45° от оси x. Из нашего предыдущего анализа, полагая, что v = 0,25 и c = 1, уравнение пунктирной линии одновременности составляет t — 0.25x = 0, а при v = 0, уравнение пунктирной линии одновременности есть t = 0.

В общем случае второй наблюдатель прослеживает мировую линию в пространстве-времени первого наблюдателя, описываемой как t = x/v, и набор одновременных событий для второго наблюдателя (в начале координат) описывается линией t = vx. Обратите внимание на обратное отношение угловых коэффициентов мировой линии и одновременных событий в соответствии с принципом гиперболической ортогональности.

Изоконтуры радарного времени.

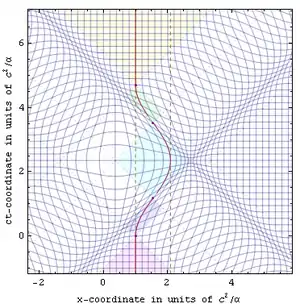
В приведённом выше вычислении преобразований Лоренца используется определение расширенной одновременности (то есть когда и где происходят события, в которых вы не участвовали), которое можно назвать как сопутствующее или «касательное к свободной системе отсчёта». Это определение естественно экстраполируется на события в гравитационно-искривлённом пространстве-времени и на ускоренных наблюдателей посредством использования радарного времени/расстояния, которое (в отличие от определения касательного к свободной системе отсчёта для ускоренных систем) присваивает уникальное время и положение для любого события[16].

Определение расширенной одновременности через радарное время дополнительно облегчает визуализацию того, как ускорение искривляет пространство-время для путешественников в отсутствие каких-либо гравитирующих объектов. Это проиллюстрировано на рисунке справа, в котором показаны изоконтуры радарного времени/местоположения для событий в плоском пространстве-времени, по представлению путешественника (красная траектория), движущегося с ускорением. Одной из особенностью этого подхода является то, что время и место удалённых событий не определены полностью до тех пор, пока свет от такого события не достигнет нашего путешественника.

• Релятивистское замедление времени
• Парадокс шеста и сарая
• Прецессия Томаса
• Парадокс Эренфеста
• Синхронизация Эйнштейна
• Аргумент Ритдейка-Патнэма