Скобка Пуассона

Ско́бки Пуассо́на[1] (также возможно ско́бка Пуассо́на[2] и скобки Ли) — оператор, играющий центральную роль в определении эволюции во времени динамической системы. Эта операция названа в честь С.-Д. Пуассона. Рассматривался С. Пуассоном в 1809 году[3], затем забыт и переоткрыт К. Якоби.

Скобки Пуассона векторных полей

Пусть $v$ и $u$ — векторные поля на гладком многообразии $M$ , $L_{v}$ — оператор производной Ли по направлению векторного поля $v$ . Коммутатор операторов $L_{v}$ и $L_{u}$ есть дифференциальный оператор первого порядка, поэтому существует такое векторное поле $[v,u]$ , для которого[4][Notes 1]

L_{v}L_{u}-L_{u}L_{v}\equiv [L_{v},L_{u}]=L_{[v,u]}

Компоненты векторного поля $[v,u]$ в произвольной системе координат выражаются через компоненты $v$ и $u$ по формуле

$[v,u]_{i}=\sum _{j}v_{j}{\frac {\partial u_{i}}{\partial x_{j}}}-u_{j}{\frac {\partial v_{i}}{\partial x_{j}}}.$

Таким образом, поле $[v,u]$ не зависит от системы координат $(x_{1},...,x_{n}),$ которая используется в формуле.

Это векторное поле называется коммутатором, скобками Ли или скобками Пуассона двух векторных полей. Явное выражение для скобок Ли полей:

[v,u]=L_{v}u

В голономном базисе оно принимает вид

[v,u]^{\mu }=v^{\alpha }\partial _{\alpha }u^{\mu }-u^{\alpha }\partial _{\alpha }v^{\mu }

Пример

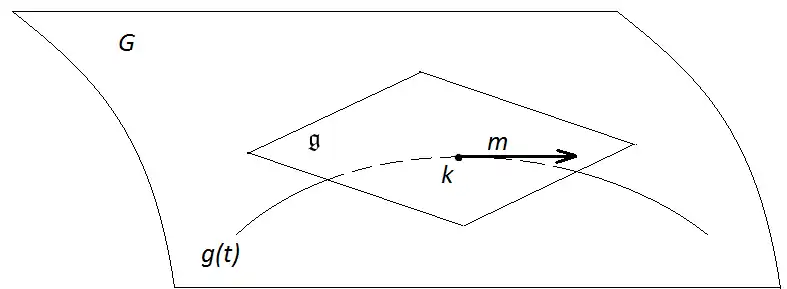
Пусть $G=\mathrm {Diff} (M)$ есть группа диффеоморфизмов многообразия $M$ . Тогда $\mathrm {ad} _{v}w=-\{v,w\},$ где $\{v,w\}$ — скобка Пуассона, $\mathrm {ad}$ — дифференциал $\mathrm {Ad}$ в единице группы. Символ $\mathrm {ad} _{v}$ обозначает образ элемента $v$ .

Пусть $t\mapsto g(t)$ является кривой, которая выходит из $k$ с начальной скоростью ${\dot {g}}=m,$ и пусть $s\mapsto h(s)$ является такой же кривой с начальной скоростью $h'=\omega .$ Тогда

$g(t)h(s)g(t)^{-1}=(k+tm+o(t))(k+s\omega +o(s))(k+tm+o(t))^{-1}=k+s[\omega +t(m\omega -\omega m)+o(t)]+o(s)$

при $t,s\rightarrow 0.$

Вектор

m

в алгебре Ли

{\mathfrak {g}}

является скоростью в единице

k

пути

g(t)

на группе Ли

G

Свойства

Все, кроме последних двух, доказываются простым подсчётом.

Линейность: ${\Big [}u,cv{\Big ]}=c{\Big [}u,v{\Big ]},\;\;\;\;c$ — функция, не зависящая от $u$ и $v$ .
Антикоммутативность: ${\Big [}u,v{\Big ]}=-{\Big [}v,u{\Big ]}$
${\Big [}w,u+v{\Big ]}={\Big [}w,u{\Big ]}+{\Big [}w,v{\Big ]}$
${\Big [}u,u{\Big ]}=0$
${\cfrac {\partial {\Big [}u,v{\Big ]}}{\partial t}}={\Big [}{\cfrac {\partial u}{\partial t}},v{\Big ]}+{\Big [}u,{\cfrac {\partial v}{\partial t}}{\Big ]}$
${\Big [}w,c{\Big ]}=0$
${\Big [}w,u\cdot v{\Big ]}={\Big [}w,u{\Big ]}v+u{\Big [}w,v{\Big ]}$
${\Big [}w,u(v_{1},\ldots ,v_{k}){\Big ]}=\sum _{l=1}^{k}{\cfrac {\partial u}{\partial v_{l}}}{\Big [}w,v_{l}{\Big ]}$
Тождество Якоби: ${\Big [}{\Big [}u,v{\Big ]},w{\Big ]}+{\Big [}{\Big [}v,w{\Big ]},u{\Big ]}+{\Big [}{\Big [}w,u{\Big ]},v{\Big ]}=0.$
Операция коммутирования задаёт на множестве векторных полей структуру алгебры Ли.

Скобки Пуассона функций

Пусть $M$ — симплектическое многообразие. Симплектическая структура $\omega$ на $M$ позволяет ввести на множестве функций на $M$ операцию скобок Пуассона, обозначаемую $\{\cdot ,\cdot \}$ или $[\cdot ,\cdot ]$ и задаваемую по правилу[1][Notes 2]

[F,G]\ {\stackrel {\text{def}}{=}}\ L_{\mathbf {F} }G\equiv dG(\mathbf {F} )\equiv \omega (\mathbf {F} ,\mathbf {G} )

где $\mathbf {F}$ (также $IdF$ ) — векторное поле, соответствующее функции Гамильтона $F$ . Оно определяется через дифференциал функции $F$ и изоморфизм между 1-формами и векторами, задаваемый (невырожденной) формой $\omega$ . Именно, для любого векторного поля $\mathbf {v}$

dF(\mathbf {v} )\ {\stackrel {\text{def}}{=}}\ \omega (\mathbf {v} ,\mathbf {F} )

Алгебра Ли функций Гамильтона

В силу кососимметричности и билинейности $\omega$ скобка Пуассона также будет кососимметричной и билинейной:

[F,G]=-[G,F]

[F,\lambda G+\mu H]=\lambda [F,G]+\mu [F,H]

Выражение

[F,[G,H]]+[G,[H,F]]+[H,[F,G]]

является линейной функцией вторых производных каждой из функций $F,G,H$ . Однако

{\begin{array}{r}[F,[G,H]]+[G,[H,F]]+[H,[F,G]]=\\-L_{Id[G,H]}F+L_{\mathbf {G} }L_{\mathbf {H} }F-L_{\mathbf {H} }L_{\mathbf {G} }F=\\\left(-L_{Id[G,H]}+L_{[\mathbf {G} ,\mathbf {H} ]}\right)F\end{array}}

Это выражение не содержит вторых производных $F$ . Аналогично, оно не содержит вторых производных $G$ и $H$ , а потому

[F,[G,H]]+[G,[H,F]]+[H,[F,G]]=0

то есть скобки Пуассона удовлетворяют тождеству Якоби. Таким образом, скобки Пуассона позволяют ввести на множестве функций на $M$ структуру алгебры Ли. Из тождества Якоби следует, что для любой функции $H$

L_{Id[F,G]}H=L_{[\mathbf {F} ,\mathbf {G} ]}H

,

то есть

Id[F,G]=[\mathbf {F} ,\mathbf {G} ]

— операция построения гамильтонова векторного поля по функции задаёт гомоморфизм алгебры Ли функций в алгебру Ли векторных полей.

Свойства

Скобки Пуассона невырождены:

\forall F\not \equiv 0\ \exists H:[F,H]\neq 0

Скобки Пуассона удовлетворяют тождеству Лейбница:

[F,GH]=[F,G]H+G[F,H]

Функция $F$ является первым интегралом для гамильтоновой системы с гамильтонианом $H$ тогда и только тогда, когда $[F,H]=0$
Скобка Пуассона двух первых интегралов системы — снова первый интеграл (следствие тождества Якоби).
Рассмотрим эволюцию гамильтоновой системы с функцией Гамильтона $H$ , заданной на многообразии $M$ . Полная производная по времени от произвольной функции $f\colon M\times \mathbb {R} \to \mathbb {R}$ запишется в виде

{\begin{array}{cl}{\frac {d}{dt}}f=&{\frac {\partial f}{\partial t}}+{\dot {q}}{\frac {\partial f}{\partial q}}+{\dot {p}}{\frac {\partial f}{\partial p}}=\\&{\frac {\partial f}{\partial t}}+L_{\mathbf {H} }f=\\&{\frac {\partial }{\partial t}}f+[H,f]\end{array}}

В канонических координатах $(q_{i},p_{j})$ скобки Пуассона принимают вид[Notes 3]

[f,g]=\sum _{i=1}^{N}\left({\frac {\partial f}{\partial p_{i}}}{\frac {\partial g}{\partial q^{i}}}-{\frac {\partial f}{\partial q^{i}}}{\frac {\partial g}{\partial p_{i}}}\right)

[5]

Философское значение

Скобки Пуассона сыграли важную эвристическую роль при создании квантовой механики методом классической аналогии между классическими и квантовыми скобками Пуассона.[6][7][8][9]

Примечания

Некоторые авторы [Арнольд] используют определение с противоположным знаком, при этом также изменяется знак в определении скобок Пуассона функций (см. ниже). Этот подход продиктован, по-видимому, стремлением сохранить как естественные геометрические определения гамильтоновых полей и их свойств, так и традиционную форму записи скобок Пуассона в координатах. Однако при этом разрушается естественная симметрия между коммутаторами производных Ли, векторов и функций. Дальнейшие проблемы возникают при переходе к общим понятиям дифференциальной геометрии (формы, векторнозначные формы, различные дифференцирования), где отсутствие указанной симметрии неоправданно усложняет формулы. Поэтому в данной статье будут использованы другие определения, с оговорками.
В некоторых книгах [Арнольд] принято определение с противоположным знаком, а именно $[F,G]\ {\stackrel {def}{=}}\ dF(\mathbf {G} )={-L_{\mathbf {F} }G.}$ При этом также определяется с противоположным знаком коммутатор векторных полей (см. выше), а выражение для скобки Пуассона в координатах принимает традиционный вид, однако появляется лишний минус в выражении $L_{Id[F,G]}=-L_{[\mathbf {F} ,\mathbf {G} ]}$ и формуле для коммутатора полей.
В [Арнольд], [Гантмахер] выражение имеет противоположный знак (аналогично вышеуказанным замечаниям). Традиционно выражение записывают как в [Гантмахер].

Литература

Гантмахер Ф. Р. Лекции по аналитической механике: Учебное пособие для вузов / Под ред. Е. С. Пятницкого. — 3-е изд. — М.: ФИЗМАТЛИТ, 2005. — 264 с. — ISBN 5-9221-0067-X.
Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
Poisson S. D. Memoire sur lavariation des constantes arbitraire dans les questions de Mechanique. - Journ. Politechn. 1809 t. VIII, p. 266-344
Ivan Kolář, Peter W. Michor, Jan Slovák Natural operations in differential geometry, — Springer-Verlag, Berlin, Heidelberg, 1993. — ISBN 3-540-56235-4, ISBN 0-387-56235-4.
Ландау Л. Д, Лифшиц Е. М. Теоретическая физика. Том 1. / доктор физико-математических наук Л. П. Питаевский. — 5-е. — ФИЗМАТЛИТ, 2004. — С. 176-179. — ISBN 5-9221-0055-6.
Дирак П А М "Основные уравнения квантовой механики" УФН 122 611–621 (1977)
Дирак П. А. М. Воспоминания о необычайной эпохе. — М., Наука, 1990. — с. 20-21
Дирак П. А. М. Принципы квантовой механики. — М., Физматлит, 1960. — с. 125-130
Разумовский О. С. Скобки Пуассона как метод // Яненко Н. Н., Преображенский Н. Г., Разумовский О. С. Методологические проблемы математической физики. — Новосибирск, Наука, 1986. — с. 246-263

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[5] Некоторые авторы [Арнольд] используют определение с противоположным знаком, при этом также изменяется знак в определении скобок Пуассона функций (см. ниже). Этот подход продиктован, по-видимому, стремлением сохранить как естественные геометрические определения гамильтоновых полей и их свойств, так и традиционную форму записи скобок Пуассона в координатах. Однако при этом разрушается естественная симметрия между коммутаторами производных Ли, векторов и функций. Дальнейшие проблемы возникают при переходе к общим понятиям дифференциальной геометрии (формы, векторнозначные формы, различные дифференцирования), где отсутствие указанной симметрии неоправданно усложняет формулы. Поэтому в данной статье будут использованы другие определения, с оговорками.

[6] В некоторых книгах [Арнольд] принято определение с противоположным знаком, а именно $[F,G]\ {\stackrel {def}{=}}\ dF(\mathbf {G} )={-L_{\mathbf {F} }G.}$ При этом также определяется с противоположным знаком коммутатор векторных полей (см. выше), а выражение для скобки Пуассона в координатах принимает традиционный вид, однако появляется лишний минус в выражении $L_{Id[F,G]}=-L_{[\mathbf {F} ,\mathbf {G} ]}$ и формуле для коммутатора полей.

[7] В [Арнольд], [Гантмахер] выражение имеет противоположный знак (аналогично вышеуказанным замечаниям). Традиционно выражение записывают как в [Гантмахер].

[Gantmaher-1] Гантмахер Ф. Р. Лекции по аналитической механике: Учебное пособие для вузов / Под ред. Е. С. Пятницкого. — 3-е изд. — М.: ФИЗМАТЛИТ, 2005. — 264 с. — ISBN 5-9221-0067-X.

[Arnold-2] Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.

[3] Poisson S. D. Memoire sur lavariation des constantes arbitraire dans les questions de Mechanique. - Journ. Politechn. 1809 t. VIII, p. 266-344

[4] Ivan Kolář, Peter W. Michor, Jan Slovák Natural operations in differential geometry, — Springer-Verlag, Berlin, Heidelberg, 1993. — ISBN 3-540-56235-4, ISBN 0-387-56235-4.

[8] Ландау Л. Д, Лифшиц Е. М. Теоретическая физика. Том 1. / доктор физико-математических наук Л. П. Питаевский. — 5-е. — ФИЗМАТЛИТ, 2004. — С. 176-179. — ISBN 5-9221-0055-6.

[9] Дирак П А М "Основные уравнения квантовой механики" УФН 122 611–621 (1977)

[10] Дирак П. А. М. Воспоминания о необычайной эпохе. — М., Наука, 1990. — с. 20-21

[11] Дирак П. А. М. Принципы квантовой механики. — М., Физматлит, 1960. — с. 125-130

[12] Разумовский О. С. Скобки Пуассона как метод // Яненко Н. Н., Преображенский Н. Г., Разумовский О. С. Методологические проблемы математической физики. — Новосибирск, Наука, 1986. — с. 246-263