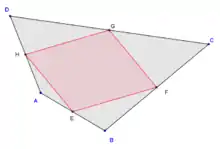
Серединный многоугольник

Серединный многоугольник (многоугольник Казнера[1][2]) — многоугольник, вершинами которого являются середины рёбер исходного многоугольника[3][4].

Серединный треугольник
Вариньонов параллелограмм

Серединный треугольник обладает тем же центроидом и теми же медианами, что и исходный треугольник. Периметр серединного треугольника равен полупериметру исходного треугольника, а площадь равна четверти площади исходного треугольника (показывается с помощью формулы Герона). Ортоцентр серединного треугольника совпадает с центром описанной окружности исходного треугольника.

В силу теоремы Вариньона серединный четырёхугольник всегда является параллелограммом, который называется вариньоновым. Если четырёхугольник является простым, то площадь параллелограмма равна половине площади исходного четырёхугольника. Периметр параллелограмма равен сумме диагоналей исходного четырёхугольника.

Примечания
  1. Kasner, 1903, с. 59.
  2. Schoenberg, 1982, с. 91, 101.
  3. Gardner, 2006, с. 36.
  4. Gardner, Gritzmann, 1999, с. 92.

Литература
  • Richard J. Gardner. Geometric tomography. — 2nd. — Cambridge University Press, 2006. — Т. 58. — (Encyclopedia of Mathematics and its Applications).
  • Richard J. Gardner, Peter Gritzmann. Discrete tomography: Foundations, Algorithms, and Applications / Gabor T.Herman, Attila Kuba. — Springer, 1999. — С. 85–114.
  • Edward Kasner. The Group Generated by Central Symmetries, with Application to Polygons // American Mathematical Monthly. — 1903. — Т. 10, вып. 3 (March). — С. 57–63. — doi:10.2307/2968300.
  • I. J. Schoenberg. Mathematical time exposures. — Mathematical Association of America, 1982. — ISBN 0-88385-438-4.
  • Elwyn R. Berlekamp, Edgar N. Gilbert, Frank W. Sinden. A Polygon Problem // American Mathematical Monthly. — 1965. — Т. 72, вып. 3 (March). — С. 233–241. — doi:10.2307/2313689.
  • J. H. Cadwell. A Property of Linear Cyclic Transformations // The Mathematical Gazette. — 1953. — Т. 37, вып. 320 (May). — С. 85–89.
  • Richard J. Clarke. Sequences of Polygons // Mathematics Magazine. — 1979. — Т. 52, вып. 2 (March). — С. 102–105. — doi:10.2307/2689847.
  • Hallard T. Croft, K. J. Falconer, Richard K. Guy. Unsolved Problems in Geometry. — Springer, 1991. — С. 76–78.
  • Gaston Darboux. Sur un problème de géométrie élémentaire // Bulletin des sciences mathématiques et astronomiques, Sér. 2. — 1878. — Т. 2, вып. 1. — С. 298–304.
  • Y. David Gau, Lindsay A. Tartre. The Sidesplitting Story of the Midpoint Polygon // Mathematics Teacher. — 1994. — Т. 87, вып. 4 (April). — С. 249–256.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.