Седлоузловая бифуркация

В теории динамических систем, седлоузловая бифуркация — локальная бифуркация, при которой пара особых точек (устойчивая и неустойчивая) сливаются в полуустойчивую особую точку (седлоузел), затем исчезающую. Единственная бифуркация, которая встречается в типичных однопараметрических семействах векторных полей на прямой неустранимым образом (т.е. является типичной бифуркацией коразмерности 1).

Нормальная форма

анимация

Рассмотрим векторное поле на прямой, имеющее особую точку. Если особая точка невырождена (производная векторного поля в ней отлична от 0), по теореме о неявной функции, она сохраняется при малых возмущениях, и бифуркации не происходит. Таким образом, простейший случай, интересный с точки зрения теории бифуркаций: первая производная равна нулю. В типичном случае, вторая производная ненулевая. Раскладывая векторное поле в ряд Тейлора и меняя при необходимости систему координат, можно считать, что коэффициент при $x^{2}$ равен -1. В этом случае векторное поле имеет вид:

{\dot {x}}=-x^{2}+o(x^{2}).\quad \quad (1)

Поскольку особая точка вырождена, векторное поле (1) не является структурно устойчивым: сколь угодно малым возмущением можно уничтожить особую точку или «развалить» её на две. Оказывается, любое невырожденное малое возмущение этого векторного поля в окрестности особой точки 0 (топологически) эквивалентно однопараметрическому семейству

{\dot {x}}=\varepsilon -x^{2}\quad \quad (2)

Иными словами, это семейство будет версальной деформацией для уравнения (1). Семейство (2) является нормальной формой седлоузловой бифуркации.

Сценарий бифуркации

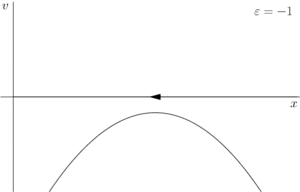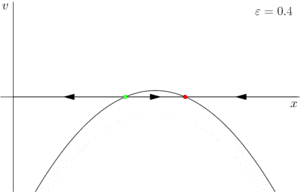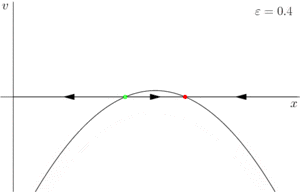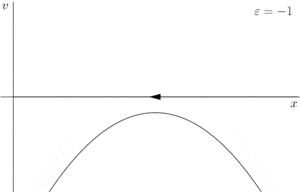
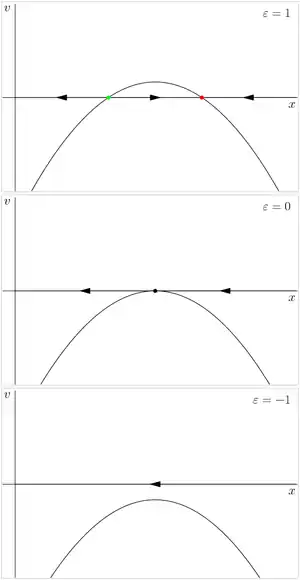
Рассмотрим семейство (2). Возможно три случая:

При $\varepsilon >0$ векторное поле имеет две особые точки: $x=\pm {\sqrt {\varepsilon }}$ . Одна из них ( $x=+{\sqrt {\varepsilon }}$ ) является устойчивой, другая ( $x=-{\sqrt {\varepsilon }}$ ) — неустойчивой.
При $\varepsilon =0$ векторное поле имеет единственную полуустойчивую негиперболическую особую точку 0.
При $\varepsilon <0$ векторное поле не имеет особых точек.

Таким образом, седлоузловая бифуркация может быть описана как процесс рождения полуустойчивой особой точки и последующего её распадения на устойчивую и неустойчивую, или наоборот — как процесс слияния устойчивой и неустойчивой особой точки в полуустойчивую с последующим её исчезновением.

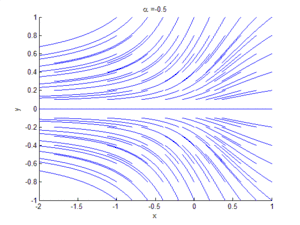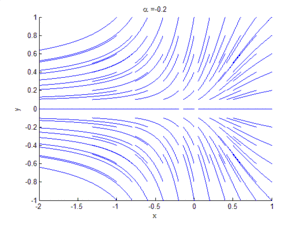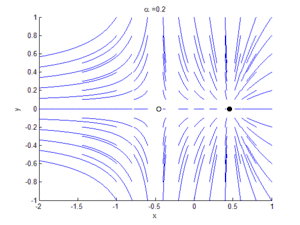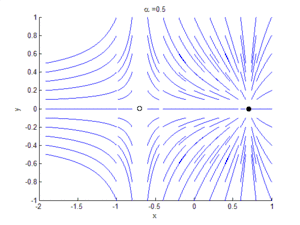
Седлоузловая бифуркация на плоскости:

\alpha =\varepsilon

Если рассматривать двумерное фазовое пространство и к уравнению (2) добавить уравнение ${\dot {y}}=-y$ , при $\varepsilon >0$ , особая точка $({\sqrt {\varepsilon }},0)$ будет устойчивым узлом, а особая точка $(-{\sqrt {\varepsilon }},0)$ — седлом. Сливаясь при $\varepsilon =0$ , они образуют особую точку с одним нулевым и одним ненулевым собственным значением, то есть седлоузел. Это и объясняет название бифуркации.

Литература

Д. Ван, Ч. Ли, Ш.-Н. Чоу. Нормальные формы и бифуркации векторных полей на плоскости. — М.: МЦНМО, 2005. — 416 с. — ISBN 5-94057-206-5.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.