Реактивная тяга
Реактивная тяга — сила, возникающая в результате взаимодействия реактивной двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией[1].
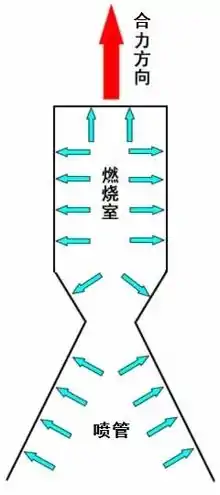
В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:
- приложена непосредственно к корпусу реактивного двигателя;
- обеспечивает передвижение реактивного двигателя и связанного с ним объекта в сторону, противоположную направлению реактивной струи[2].
Реактивное движение в природе
Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена в противоположное направление движению плода[3].
Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.
Величина реактивной тяги
Формула при отсутствии внешних сил
Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
, где
Поскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном массовым секундным расходом топлива[1].
Доказательство
До начала работы двигателей импульс ракеты и топлива был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю: , где
Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:
Произведение массы ракеты m на ускорение её движения a по определению равно силе, вызывающей это ускорение:
Уравнение Мещерского
Если же на ракету, кроме реактивной силы , действует внешняя сила , то уравнение динамики движения примет вид:
Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами , действующими на тело, но и реактивной силой , обусловленной изменением массы движущегося тела:
Формула Циолковского
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского[4]:
Релятивистское обобщение этой формулы имеет вид:
, где — скорость света.
Примечания
- Военный энциклопедический словарь ракетных войск стратегического назначения / Министерство обороны РФ.; Гл.ред.: И. Д. Сергеев, В. Н. Яковлев, Н. Е. Соловцов. — Москва: Большая Российская энциклопедия, 1999. — С. 456,476-477. — ISBN 5-85270-315-X.
- Реактивная тяга Глоссарий.ru
- Реактивное движение. Класс!ная физика для любознательных
- Двигатели — Реактивное движение Архивная копия от 16 июня 2007 на Wayback Machine ASTROLAB.ru
