Расстояние Минковского

Расстояние Минковского (метрика Минковского) — параметрическая метрика на евклидовом пространстве, которую можно рассматривать как обобщение евклидова расстояния и расстояния городских кварталов. Названа в честь немецкого математика Германа Минковского, впервые систематически изучившего данное семейство функций расстояния.

Расстояние Минковского порядка ${\displaystyle p}$ между двумя точками ${\displaystyle x,y\in \mathbb {R} ^{n}}$ определяется как[1]

${\displaystyle \rho (x,y)=\left(\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{1/p}}$.

Для ${\displaystyle p\geqslant 1}$ расстояние Минковского является метрикой вследствие неравенства Минковского.

Для ${\displaystyle p<1}$ расстояние не является метрикой, поскольку нарушается неравенство треугольника.

При ${\displaystyle p=\infty }$ метрика обращается в расстояние Чебышёва[2].

В приложениях чаще всего используют функцию расстояния с параметром ${\displaystyle p}$, равным 1 (расстояние городских кварталов) или 2 (евклидова метрика)[3].

Единичная окружность при различных значениях параметра ${\displaystyle p}$ расстояния Минковского

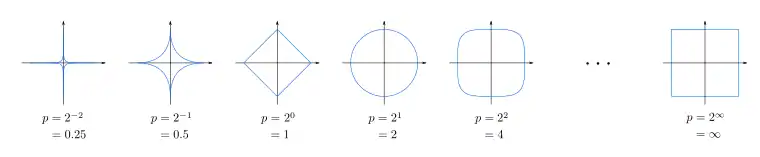
Схожая параметрическая конструкция в функциональном анализе — норма на пространствах ${\displaystyle L^{p}}$, которая вводится подобным образом[4].