Особое решение

Осо́бое реше́ние обыкновенного дифференциального уравнения — решение, в любой окрестности каждой точки которого нарушается единственность решения задачи Коши для этого уравнения.

Определение

Рассмотрим уравнение

F(x,y,y')=0,\ \ \ (1)

где $F(x,y,p)$ — $C^{1}$ -гладкая функция в некоторой области $G\subseteq {\mathbb {R} ^{3}}_{(x,y,p)}$ . Решение уравнения (1) $y=\psi (x),x\in \mathrm {I} \subseteq \mathbb {R} ,$ называется особым решением, если каждая точка $(x_{0},\psi (x_{0})),x_{0}\in \mathrm {I} ,$ соответствующем ему интегральной кривой является точкой локальной неединственности решения задачи Коши с начальным условием $y(x_{0})=\psi (x_{0})$ .

Свойства

Особое решение $y=\psi (x),x\in \mathrm {I}$ , уравнения (1) геометрически означает, что интегральная кривая $y=\psi (x)$ в каждой своей точке касается некоторой другой интегральной кривой уравнения (1) и не совпадает с ней в некоторой окрестности этой точки, то есть является огибающей семейства интегральных кривых уравнения (1).

Особое решение уравнения (1), если оно существует, всегда является дискриминантной кривой этого уравнения[1](точнее, оно всегда является частью дискриминантной кривой: последняя может иметь несколько ветвей с разными свойствами). Обратное не верно: дискриминантная кривая не обязательно является решением уравнения (а если является, то не обязательно особым) [2]. Так, например, дискриминантная кривая уравнения Чибрарио $(y')^{2}=x$ является не решением, а геометрическим местом точек возврата его интегральных кривых.

Поэтому для практического отыскания особых решений уравнения нужно сначала найти его дискриминантную кривую, а затем проверить, является ли она (каждая её ветвь, если их несколько) особым решением уравнения (1), или нет[2].

Примеры

Особые решения дифференциальных уравнений (жирные линии): уравнения Клеро (слева) и уравнения

(y')^{2}=y

(справа).

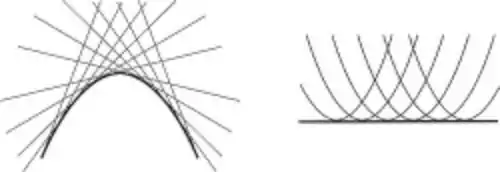
1. Простыми примерами дифференциальных уравнений, имеющих особые решения, являются уравнение Клеро и уравнение $(y')^{2}=y$ , неособые решения которого задаются формулой $y={\frac {1}{4}}(x-c)^{2}$ с постоянной интегрирования $c$ , а особое решение имеет вид $y=0$ .

2. Дискриминантная кривая уравнения $(y')^{2}=4y^{3}(1-y)$ состоит из двух непересекающихся ветвей: $y=1$ и $y=0$ . Обе они являются решениями этого уравнения. Однако первая из них является особым решением, а вторая — нет: в каждой точке линии $y=1$ она касается какой-либо другой интегральной кривой этого уравнения, а к линии $y=0$ интегральные кривые лишь приближаются асимптотически при $x\to \infty$ [3].

Примечания

Дискриминантная кривая уравнения (1) — это кривая на плоскости переменных $(x,y)$ , задаваемая уравнениями $F(x,y,p)=F_{p}(x,y,p)=0$ .
Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — М.: УРСС, 2007, гл. 2, параграф 8.
Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — М.: УРСС, 2007, гл. 2, параграф 8, пример 5.

Литература

Арнольд В. И. Дополнительные главы теории обыкновенных дифференциальных уравнений. — М.: Наука, 1978.
Арнольд В. И. Геометрические методы в теории обыкновенных дифференциальных уравнений. — Ижевск: Изд-во Удмуртского гос. ун-та, 2000.
Романко В. К. Курс дифференциальных уравнений и вариационного исчисления. — М.: Физматлит, 2001.
Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — М.: УРСС, 2004, 2007.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Дискриминантная кривая уравнения (1) — это кривая на плоскости переменных $(x,y)$ , задаваемая уравнениями $F(x,y,p)=F_{p}(x,y,p)=0$ .

[autogenerated1-2] Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — М.: УРСС, 2007, гл. 2, параграф 8.

[3] Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — М.: УРСС, 2007, гл. 2, параграф 8, пример 5.