Магический шестиугольник
Магический шестиугольник или магический гексагон порядка — набор чисел, расположенный в центрированной шестиугольной решётке со стороной таким образом, что сумма чисел в каждой строке во всех направлениях равна некоей магической константе
 |
 |
| Порядок n = 1 |
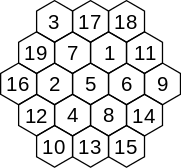
Порядок n = 3 |
Обычный магический шестиугольник может быть только порядка (случай тривиален, и здесь речь о нём идти не будет) или и может содержать числа от единицы до Более того, если не считать зеркальных, существует только один магический шестиугольник порядка
Магический шестиугольник публиковался много раз как новое явление. Первооткрывателем, возможно, является Эрнст фон Хасельберг (нем. Ernst von Haselberg) в 1887 году.
Доказательство единственности
Докажем, что существуют магические шестиугольники только порядка и
Вычислим магическую константу С одной стороны, гексагон содержит числа от единицы до (это легко доказать, разложив фигуру на три параллелограмма). То есть, сумма всех чисел в гексагоне
С другой стороны, есть рядов (например, вертикальных), которые включают в себя все числа в шестиугольнике. Так как сумма чисел в каждом ряду равна то во всём шестиугольнике будет
Приравняв суммы, получим, что
Слева стоит целое число. Значит, справа должно тоже быть целое число.
Значит, — это целое число, что возможно только при и
QED.
Аномальные магические шестиугольники
Хотя нормальных магических шестиугольников порядка, отличного от не существует, существуют аномальные магические шестиугольники иных порядков.
Аномальными магическими шестиугольниками назовём шестиугольники, образованные по указанным выше правилам, однако, начинающие отсчёт чисел не от единицы, а от иного числа.
| 14 33 30 34 39 6 24 20 22 37 13 11 8 25 17 21 23 7 9 3 10 38 36 4 5 12 28 26 35 16 18 27 15 19 31 29 32 | 41 51 63 45 44 64 25 40 46 35 34 23 20 10 56 27 42 66 55 38 19 9 6 22 48 47 61 58 18 11 8 7 13 15 53 52 37 14 16 30 12 24 59 57 32 29 21 17 39 49 31 36 62 28 54 33 43 26 60 65 50 | 56 61 70 67 51 55 45 36 48 53 68 74 37 26 29 27 39 73 62 42 33 19 16 31 38 64 58 57 22 20 15 18 23 43 49 63 47 28 21 17 30 34 65 71 35 24 32 25 46 72 59 44 40 41 52 69 54 60 75 66 50 |
| Порядок 4 Начинается с и кончается | Порядок 5 Начинается с и кончается . | Порядок 5 Начинается с и кончается . |
Магический гексагон порядка , начинающийся с и кончающийся () был создан Louis Hoelbling 11 октября 2004 года.

Гексагон порядка , начинающийся с 2 и кончающийся 128 () был создан Arsen Zahray 22 марта 2006 года.
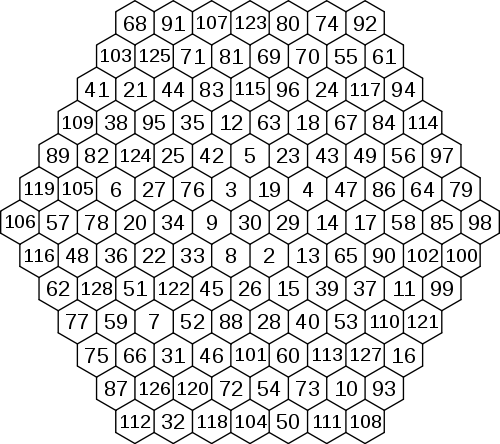
Наибольший из известных на данный момент гексагон подярка , начинающийся с −84 и кончающийся 84 () был создан Louis K. Hoelbling 5 февраля 2006 года.

См. также
Примечания
Литература
- Baker. J. E. and King, D. R. (2004) «The use of visual schema to find properties of a hexagon» Visual Mathematics, Volume 5, Number 3
- Baker, J. E. and Baker, A. J. (2004) «The hexagon, nature’s choice» Archimedes, Volume 4