Линейно связное пространство
Лине́йно свя́зное простра́нство — это топологическое пространство, в котором любые две точки можно соединить непрерывной кривой.
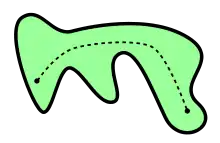
Линейно связное подмножество евклидовой плоскости
Определения
- Рассмотрим отрезок числовой прямой с определённой на нём стандартной топологией вещественной прямой. Пусть также дано топологическое пространство Тогда последнее называется линейно связным[1], если для любых двух точек найдётся непрерывное отображение такое, что
- Пусть дано подмножество . Тогда на нём естественным образом определяется топология , индуцированная . Если пространство линейно связно, то подмножество также называется линейно связным в [2].
Связанные определения
- Каждое линейно связное подмножество пространства содержится в некотором максимальном линейно связном подмножестве. Такие максимальные связные подмножества называются компонентами линейной связности пространства [2].
- Пространство, в котором каждая компонента линейной связности состоит из одной точки, называется вполне линейно несвязным (по аналогии с вполне несвязным пространством).
- Если существует база топологии пространства , состоящая из линейно связных открытых множеств, тогда топология пространства и само пространство (в этой топологии) называются локально линейно связными[3].
Примеры
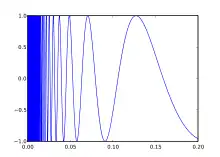
Замыкание графика функции — пример связного, но не линейно связного множества.
- Прямая, окружность, выпуклое подмножество евклидова пространства — примеры линейно связных пространств[4].
- Замыкание графика функции при — пример связного пространства, которое не является линейно связным. Это пространство имеет две компоненты линейной связности: график функции при x > 0, и отрезок на оси ординат[5].
- Псевдодуга — пример связного, но вполне линейно несвязного пространства.
Свойства
- Всякое линейно связное пространство связно. Обратное неверно[1].
- Конечное топологическое пространство линейно связно тогда и только тогда, когда оно связно.
- Непрерывный образ линейно связного пространства линейно связен[5].
- Если пространство линейно связно и , то гомотопические группы и изоморфны, причем этот изоморфизм определяется однозначно с точностью до внутреннего автоморфизма [6].
Линейная связность на числовой прямой
Будем считать, что , а — стандартная топология числовой прямой. Тогда[5]
- Подмножество линейно связно тогда и только тогда, когда
- то есть любые две точки входят в него вместе с соединяющим их отрезком.
- Любое линейно связное подмножество числовой прямой является конечным или бесконечным открытым, полуоткрытым или замкнутым интервалом:
- Подмножество числовой прямой линейно связно тогда и только тогда, когда оно связно.
Обобщение
Многомерным обобщением линейной связности является -связность (связность в размерности ). Пространство называется связным в размерности , если любые два отображения -мерной сферы в , где , гомотопны. В частности, -связность — это то же, что линейная связность, а -связность — то же, что односвязность[7].
Примечания
- Фоменко, Фукс, 1989, с. 24.
- Виро и др., 2012, с. 86.
- Виро и др., 2012, с. 229.
- Виро и др., 2012, с. 85—86.
- Виро и др., 2012, с. 87.
- Фоменко, Фукс, 1989, с. 51.
- Фоменко, Фукс, 1989, с. 49.
Литература
- Фоменко, А. Т., Фукс, Д. Б. Курс гомотопической топологии. — М.: Наука, 1989. — 528 с. — ISBN 5-02-013929-7.
- Виро, О. Я., Иванов, О. А., Нецветаев, Н. Ю., Харламов, В. М. Элементарная топология. — 2-е изд., исправл.. — М.: МЦНМО, 2012. — ISBN 978-5-94057-894-9.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.