Локально линейно связное пространство

Локально линейно связное пространство ― топологическое пространство, в котором для любой точки и любой её окрестности имеется меньшая линейно связная окрестность. Другими словами, у каждой точки найдётся база окрестностей, состоящая из линейно связных множеств.

Подмножество топологического пространства называется локально линейно связным, если оно вместе со своей индуцированной топологией образует локально линейно связное пространство.

Свойства

Локально линейно связное пространство является локально связным, обратное не всегда выполнено.
Локально линейно связное пространство не обязано быть линейно связным, однако и обратное не всегда верно.

Примеры

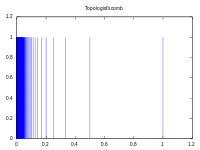
Гребёнка — линейно связное, но не локально линейно связное пространство

Евклидово пространство $\mathbb {R} ^{n}$ со стандартной топологией является локально линейно связным.
Пространство $[0,1]\cup [2,3]$ с топологией, индуцированной стандартной топологией действительной прямой, является локально линейно связным, однако не является линейно связным.
Гребёнка, то есть подмножество евклидовой плоскости

\left(\{0\}\times [0,1]\right)\cup \left([0,1]\times \{0\}\right)\cup \left(\{1/n\mid n\in \mathbb {N} \}\times [0,1]\right)

с топологией, индуцированной стандартной, является, очевидно, линейно связным пространством, однако локально линейно связным не является: любая достаточно малая (радиуса меньше $1/2$ ) окрестность точки $(0,1/2)$ не является линейно связной.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.