Лемма Витали о покрытиях
Лемма Витали о покрытиях — комбинаторногеометрический результат. Широко используется в теории меры.
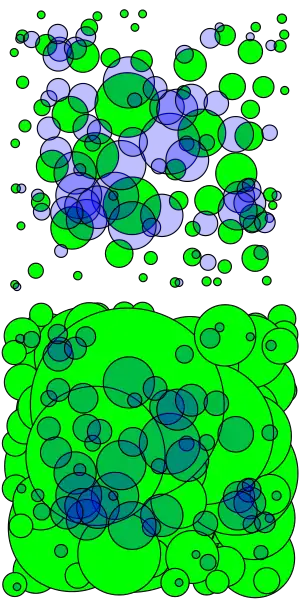
Эта лемма используется в доказательстве теоремы Витали о покрытиях, но также представляет самостоятельный интерес. Названа в честь итальянского математика Джузеппе Витали.
Формулировка
Конечная версия
Пусть — конечный набор шаров, содержащихся в d-мерном евклидовом пространстве Rd (или, в более общем случае, в произвольном метрическом пространстве). Тогда существует подмножество из этих шаров, в котором шары попарно не пересекаются, и выполняется
где обозначает шар с тем же центром, что и у , но с утроенным радиусом.
Бесконечная версия
Пусть — произвольный (счётный или несчётный) набор шаров в Rd (или, более общо, в метрическом пространстве), такой что
где обозначает радиус шара Bj. Тогда для любого существует счётное подмножество
попарно непересекающихся шаров, таких что
Замечания
- В бесконечной версии лемма перестаёт быть верной, если радиусы не ограничены: например, это неверно для бесконечного набора концентрических шаров с целыми положительными радиусами.
- В самом общем случае, для произвольного метрического пространства, выбор максимальной непересекающейся подколлекции шаров требует некоторой формы леммы Цорна.
Следствия
- В любом конечном наборе шаров -мерного Евклидова пространства с объёмом объединения , можно выбрать поднабор пересекающихся между собой шаров с общим объёмом не менее .
- Коэффициент не является оптимальным и оптимальное значение не известно.[1]
Вариации и обобщения
- Вместо шаров можно брать другие области с довольно слабыми условиями.[2]
- Лемма Безиковича — аналог леммы Витали. Она применима для произвольных мер, но только для простых метрических пространств включая евклидово пространство в то время как Лемма Витали применима на произвольных метрических пространствах для мер обладающих свойством удвоения. Последнее означает, что для некоторой вещественной константы и произвольного шара имеем
Примечания
- The optimal constant in Vitali covering lemma
- Федерер Г. Геометрическая теория меры. — 1987. — 760 с.
Литература
- Vitali, Giuseppe (1908), Sui gruppi di punti e sulle funzioni di variabili reali, Atti dell'Accademia delle Scienze di Torino Т. 43: 75–92, <http://www.archive.org/stream/attidellarealeac43real#page/228/mode/2up>.
- И. П. Натансон. Теория функций вещественной переменной.