Коническая комбинация

Коническая комбинация (коническая сумма, взвешенная сумма) — операция над конечным набором векторов ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ в евклидовом пространстве, сопоставляющая этому набору вектор вида:

${\displaystyle \alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}$,

где все числа ${\displaystyle \alpha _{i}}$ удовлетворяют условию ${\displaystyle \alpha _{i}\geqslant 0}$[1][2].

Название связано с фактом, что коническая сумма векторов определяет конус (возможно, в подпространстве меньшей размерности).

Коническая оболочка — множество всех конических комбинаций для данного множества ${\displaystyle S}$, обозначается ${\displaystyle \operatorname {cone} (S)}$[1] или ${\displaystyle \operatorname {coni} (S)}$[2]. То есть:

${\displaystyle \operatorname {coni} (S)=\left\lbrace \sum _{i=1}^{k}\alpha _{i}x_{i}\;{\Big |}\;x_{i}\in S,\,\alpha _{i}\in \mathbb {R} ,\,\alpha _{i}\geq 0,i,k=1,2,\dots \right\rbrace }$.

По определению начало координат принадлежит всем коническим оболочкам.

Коническая оболочка множества ${\displaystyle S}$ является выпуклым множеством. Фактически она является пересечением всех выпуклых конусов, содержащих ${\displaystyle S}$, объединённым с началом координат[1]. Если ${\displaystyle S}$ является компактным пространством (в частности, если оно состоит из конечного числа точек), добавление начала координат к пересечению всех выпуклых конусов не требуется.

Если поделить каждый коэффициент конической комбинации на сумму всех её коэффициентов, то станет ясно, что всякая ненулевая коническая комбинация представляет собой масштабированную выпуклая комбинация[1]. В этой связи конические комбинации и конические оболочки могут рассматриваться как выпуклые комбинации и выпуклые оболочки в проективном пространстве.

Конической оболочкой окружности, проходящей через начало координат, является открытая верхняя полуплоскость плюс начало координат

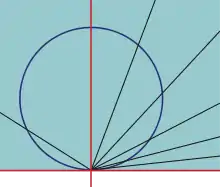
Хотя выпуклая оболочка компактного множества также является компактным множеством, для конической оболочки это неверно, так как в общем случае она не ограничена. Более того, коническая оболочка компакта даже не обязательно будет замкнутым множеством — контрпримером служит сфера, проходящая через начало координат, конической оболочкой которой является открытое полупространство плюс начало координат. Однако если ${\displaystyle S}$ является непустым компактным множеством, не содержащим начало координат, коническая оболочка множества ${\displaystyle S}$ является замкнутым множеством[1].