Квартика Люрота

Квартика Люрота (кривая четвёртой степени Люрота) — это несингулярная плоская кривая четвёртой степени, содержащая 10 вершин пятиугольной звезды (пентаграммы), не обязательно правильной. Квартики Люрота ввёл Якоб Люрот[1].

Некоторые примеры квартик Люрота

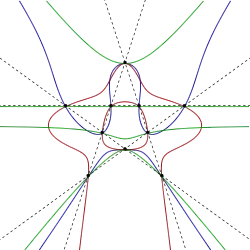
Свойства

Люрот первым обратил внимание в 1868, что, если квартика описывает пятиугольную звезду, она описывает бесконечно много других пятиугольных звёзд[2].

Морлей[3] показал, что квартики Люрота образуют открытое подмножество гиперповерхности степени 54, называемой гиперповерхностью Люрота, в пространстве P14 всех квартик. Уравнение этой гиперповерхности называется инвариантом Люрота, но оно остаётся неизвестным[2]. Гиперповерхность Люрота состоит полностью из квартик, так что пределы (когда пятиугольник вырождается) также теперь называются квартиками Люрота[2].

Бёнинг и фон Ботнер[4] доказали, что пространство модулей квартик Люрота рационально.

Квартика Люрота тесно связана с квартикой Клебша[5] — она является проективным ковариантом этой кривой[6].

Примечания
  1. Lüroth, 1869.
  2. Ottaviani, 2012, с. 2.
  3. Morley, 1919.
  4. Böhning, von Bothmer, 2011.
  5. Ottaviani, 2012, с. 7.
  6. Morley, 1919, с. 348.

Литература
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.