Дерево Тремо

Дерево Тремо неориентированного графа G — это остовное дерево графа G с выделенным корнем со свойством, что любые две смежные вершины в графе G связаны друг с другом отношением предок/потомок. Все деревья поиска в глубину и все гамильтоновы пути являются деревьями Тремо. Деревья Тремо названы именем Чарльза Пьера Тремо, французского автора 19-го века, который использовал вариант поиска в глубину как стратегию выхода из лабиринта[1][2]. Деревья Тремо также называют нормальными остовными деревьями, особенно в контексте бесконечных графов[3].

В конечных графах, хотя поиск в глубину сам по себе изначально последователен, деревья Тремо могут быть построены рандомизированным параллельным алгоритмом с классом сложности RNC. Деревья Тремо можно использовать для определения глубины дерева графа и как часть критерия планарности для проверки, является ли граф планарным. Описание деревьев Тремо одноместной логикой графов второго порядка позволяет распознать эффективно свойства графа, зависимые от ориентации, для графов с ограниченной древесной шириной при использовании теоремы Курселя.

Не любой бесконечный граф имеет дерево Тремо и графы, такого дерева не имеющие, можно описать запрещёнными минорами. Дерево Тремо существует в любом графе со счётным числом вершин, даже если вариант бесконечного поиска в глубину не может успешно проверить все вершины графа. В бесконечном графе дерево Тремо должно иметь в точности один бесконечный путь для каждого луча графа и существование дерева Тремо характеризует графы, топологические пополнения которых, образованные добавлением бесконечно удалённой точки для каждого луча, являются метрическими пространствами.

Пример

В графе, показанном ниже, дерево с рёбрами 1–3, 2–3 и 3–4 является деревом Тремо, если его корнем назначить вершину 1 или вершину 2 — любое ребро графа принадлежит дереву, за исключением ребра 1–2, которое (при выборе указанного корне) соединяет пару предок-потомок.

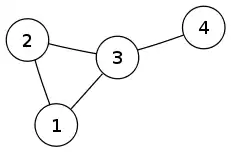
Однако, если выбрать в качестве корня для того же дерева вершину 3 или вершину 4, получим корневое дерево, не являющееся деревом Тремо, поскольку с этими корнями вершины 1 и 2 уже не будут предком/потомком.

В конечных графах

Существование

Любой конечный связный неориентированный граф имеет по меньшей мере одно дерево Тремо. Можно построить такое дерево с помощью поиска в глубину и соединения каждой вершины (отличной от начальной вершины поиска) с более ранней вершиной, из которой был получен доступ к текущей вершине. Дерево, построенное таким образом, известно как дерево поиска в глубину. Если uv является произвольным ребром в графе и u является более ранней из двух вершин, достигнутых в результате поиска, тогда v должна принадлежать поддереву потомков u в дереве поиска в глубину, поскольку поиск необходимым образом обнаружит вершину v, просматривая это дерево либо из одного из вершин поддерева, либо непосредственно из вершины u. Любое конечное дерево Тремо может быть образовано как дерево поиска в глубину — если T является деревом Тремо конечного графа и поиск в глубину исследует потомков T каждой вершины перед рассмотрением любой другой вершины, это необходимым образом генерирует T как дерево поиска в глубину графа.

Параллельное построение
Нерешённые проблемы информатики : Существует ли детерминированный параллельный алгоритм класса NC для построения деревьев Тремо?

Задача поиска дерева Тремо является P-полной, если ищется с помощью последовательного алгоритма поиска в глубину, в котором соседи каждой вершины просматриваются в порядке их номеров[4]. Тем не менее, можно найти другое дерево Тремо при использовании рандомизированного параллельного алгоритма, что показывает принадлежность построения деревьев Тремо классу сложности RNC[5]. Остаётся неизвестным, может ли дерево Тремо быть построено детерминированным параллельным алгоритмом, принадлежащим классу NC[6].

Логическое выражение

Можно выразить свойство, что множество T рёбер с выбранной корневой вершиной r образует дерево Тремо, в одноместной логике графов второго порядка, и такое выражение называется MSO2. Это свойство можно выразить как сочетание следующих свойств:

  • Граф связан рёбрами из T. Это можно выразить логически как утверждение, что для любого непустого собственного подмножества вершин графа существует ребро в T, имеющее в точности одну конечную точку в этом подмножестве.
  • T ациклично. Это можно выразить логически как утверждение, что не существует непустого подмножества C множества T, для которого каждая вершина инцидентна либо нулю, либо двум рёбрам из C.
  • Любое ребро e, не принадлежащее T, соединяет пару предок/потомок вершин в T. Это верно, когда оба конца ребра e принадлежат пути в T. Это можно выразить логически как утверждение, что для всех рёбер e существует подмножества P множества T, такое, что в точности две вершины, одна из которых r, инцидентны одному ребру в P, и оба конца дуги e инцидентны по меньшей мере одному ребру в P.

Как только дерево Тремо идентифицирована таким способом, можно описать ориентацию данного графа в одноместной логике второго порядка путём указания множества рёбер, которые ориентированы от предка к потомку. Не входящие в это множество рёбра должны быть ориентированы в обратном направлении. Эта техника позволяет описать свойства графа, использующие ориентацию, в одноместной логике второго порядка, что позволяет проверить эти свойства эффективно на графах с ограниченной древесной шириной с помощью теоремы Курселя[7].

Связанные свойства

Если граф имеет гамильтонов путь, то этот путь (с корнем в качестве одного из его концов) является также деревом Тремо. Множество неориентированных графов, для которых любое дерево Тремо имеет такой вид, состоит из циклов, полных графов и сбалансированных полных двудольных графов[8].

Деревья Тремо тесно связаны с концепцией глубины дерева. Глубина дерева графа G может быть определена как наименьшее число d, такое, что G может быть вложено в виде подграфа графа H, который имеет дерево Тремо T глубины d. Ограниченная глубина дерева в семействе графов эквивалентна существованию пути, который не может появиться в качестве минора графа в семействе. Много сложных вычислительных задач на графах имеют фиксированно-параметрически разрешимые алгоритмы, если параметризовать глубиной дерева[9].

Деревья Тремо играют также ключевую роль в критерии планарности Де Фрейсекса — Розенштиля для проверки, является ли граф планарным. Согласно этому критерию граф G планарен, если для любого дерева Тремо T графа G оставшиеся рёбра можно расположить слева и справа от дерева, что предотвращает пересечение рёбер (по этой причине иногда можно видеть название «ЛП алгоритм» — аббревиатура Левый/Правый)[10][11].

В бесконечных графах

Существование

Не любой бесконечный граф имеет нормальное остовное дерево. Например, полный граф на несчётном множестве вершин не имеет нормального остовного дерева — такое дерево в полном графе может быть только путём, но путь имеет лишь счётное число вершин. Однако любой граф на счётном множестве вершин имеет нормальное остовное дерево[3].

Даже в счётных графах поиск в глубину может оказаться неуспешным при просмотре всего графа[3], и не любое нормальное остовное дерево может быть образовано поиском в глубину — чтобы быть деревом поиска в глубину, счётное нормальное остовное дерево должно иметь только один бесконечный путь или один узел с бесконечным числом соседей (но не оба случая одновременно).

Миноры

Если бесконечный граф G имеет нормальное остовное дерево, то такой имеет и любой связный минор графа G. Отсюда следует, что графы, имеющие нормальные остовные остовные деревья, можно описать запрещёнными минорами. Один из двух классов запрещённых миноров состоит из двудольных графов, в которых одна доля счётна, а другая несчётна, и любая вершина имеет бесконечную степень. Другой класс запрещённых миноров состоит из определённых графов, полученных из деревьев Ароншайна[12].

Детали этого описания зависят от выбора аксиоматики теории множеств, используемой в формализации математики. В частности, в моделях теории множеств, в которых верна аксиома Мартина, а континуум-гипотеза не верна, класс двудольных графов может быть заменён одним запрещённым минором. Однако для моделей, в которых континуум-гипотеза верна, этот класс содержит графы, которые несравнимы в упорядочении миноров[13].

Лучи и метризуемость

Нормальные остовные деревья тесно связаны с лучами бесконечного графа, классами эквивалентности бесконечных путей, которые идут в одном и том же направлении. Если граф имеет нормальное остовное дерево, это дерево должно иметь в точности один бесконечный путь для каждого луча графа[14].

Бесконечный граф можно использовать для образования топологического пространства, если рассматривать граф сам по себе как симплициальный комплекс и добавить бесконечно удалённую точку для каждого луча графа. С такой топологией граф имеет нормальное остовное дерево тогда и только тогда, когда его множество вершин можно разбить на счётное объединение замкнутых множеств. Кроме того, это топологическое пространство может быть представлено метрическим пространством тогда и только тогда, когда граф имеет нормальное остовное дерево[14].

Примечания
  1. Even, 2011, с. 46–48.
  2. Sedgewick, 2002, с. 149–157.
  3. Soukup, 2008, с. 193 Theorem 3.
  4. Reif, 1985, с. 229–234.
  5. Aggarwal, Anderson, 1988, с. 1–12.
  6. Karger, Motwani, 1997, с. 255–272.
  7. Courcelle, 1996, с. 33–62.
  8. Chartrand, Kronk, 1968, с. 696–700.
  9. Nešetřil, Ossona de Mendez, 2012, с. 115–144.
  10. de Fraysseix, Rosenstiehl, 1982, с. 75–80.
  11. de Fraysseix, Ossona de Mendez, Rosenstiehl, 2006, с. 1017–1029.
  12. Diestel, Leader, 2001, с. 16–32.
  13. Bowler, Geschke, Pitz, 2016.
  14. Diestel, 2006, с. 846–854.

Литература
  • Shimon Even. Graph Algorithms. — 2nd. — Cambridge University Press, 2011. — С. 46–48. — ISBN 978-0-521-73653-4.
  • Robert Sedgewick. Algorithms in C++: Graph Algorithms. — 3rd. — Pearson Education, 2002. — С. 149–157. — ISBN 978-0-201-36118-6.
    • Роберт Седжвик. Часть 5. Алгоритмы на графах // Фундаментальные алгоритмы на C. — Москва, Санкт-Петербург, Киев: DiaSoft, 2003. — ISBN 5-93772-083-0.
  • John H.Reif. Depth-first search is inherently sequential. — Information Processing Letters. — 1985. — Т. 20. — С. 229–234. — doi:10.1016/0020-0190(85)90024-9.
  • Aggarwal A., Anderson R. J. A random NC algorithm for depth first search // Combinatorica. — 1988. — Т. 8, вып. 1. — С. 1–12. — doi:10.1007/BF02122548.
  • David R. Karger, Rajeev Motwani. An NC algorithm for minimum cuts. — SIAM Journal on Computing. — 1997. — Т. 26. — С. 255–272. — doi:10.1137/S0097539794273083.
  • Bruno Courcelle. On the expression of graph properties in some fragments of monadic second-order logic // Proc. Descr. Complex. Finite Models / Neil Immerman, Phokion G. Kolaitis. — Amer. Math. Soc., 1996. — Т. 31. — С. 33–62. — (DIMACS).
  • Gary Chartrand, Hudson V. Kronk. Randomly traceable graphs // SIAM Journal on Applied Mathematics. — 1968. — Т. 16. — С. 696–700.
  • Jaroslav Nešetřil, Patrice Ossona de Mendez. Chapter 6. Bounded height trees and tree-depth // Sparsity: Graphs, Structures, and Algorithms. — Heidelberg: Springer, 2012. — Т. 28. — С. 115–144. — (Algorithms and Combinatorics). — ISBN 978-3-642-27874-7. — doi:10.1007/978-3-642-27875-4.
  • Hubert de Fraysseix, Pierre Rosenstiehl. A depth-first-search characterization of planarity // Graph theory (Cambridge, 1981). — Amsterdam: North-Holland, 1982. — Т. 13. — С. 75–80. — (Ann. Discrete Math.).
  • Hubert de Fraysseix, Patrice Ossona de Mendez, Pierre Rosenstiehl. Trémaux trees and planarity // International Journal of Foundations of Computer Science. — 2006. — Т. 17, вып. 5. — С. 1017–1029. — doi:10.1142/S0129054106004248.
  • Lajos Soukup. Infinite combinatorics: from finite to infinite // Horizons of combinatorics. — Berlin: Springer, 2008. — Т. 17. — С. 189–213. — (Bolyai Soc. Math. Stud.). — ISBN 978-3-540-77199-9. — doi:10.1007/978-3-540-77200-2_10.
  • Reinhard Diestel, Imre Leader. Normal spanning trees, Aronszajn trees and excluded minors // Journal of the London Mathematical Society. — 2001. — Т. 63, вып. 1. — С. 16–32. — doi:10.1112/S0024610700001708.
  • Nathan Bowler, Stefan Geschke, Max Pitz. Minimal obstructions for normal spanning trees. — 2016. — arXiv:1609.01042.
  • Reinhard Diestel. End spaces and spanning trees // Journal of Combinatorial Theory. — 2006. — Т. 96, вып. 6. — С. 846–854. — doi:10.1016/j.jctb.2006.02.010.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.