Граф Габриэля

Граф Габриэля множества ${\displaystyle S}$ точек двумерного пространства выражает понятие близости этих точек. Формально, это граф ${\displaystyle G}$ с вершинами ${\displaystyle S}$, в котором любые точки ${\displaystyle p\in S}$ и ${\displaystyle q\in S}$ смежны, когда они различны, то есть ${\displaystyle p\neq q}$, и замкнутый круг с отрезком ${\displaystyle {\overline {pq}}}$ в качестве диаметра не содержит других элементов множества ${\displaystyle S}$.

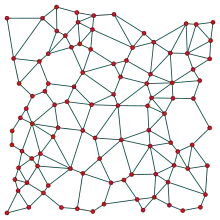
Граф Габриэля 100 случайных точек

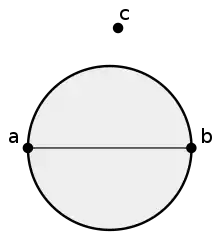
Точки ${\displaystyle a}$ и ${\displaystyle b}$ являются габриэлевыми соседями, так как ${\displaystyle c}$ лежит вне окружности с диаметром, представленным ребром ${\displaystyle ab}$.

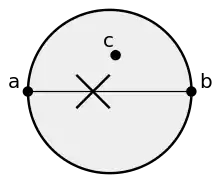
Наличие точки ${\displaystyle c}$ внутри окружности мешает точкам ${\displaystyle a}$ и ${\displaystyle b}$ быть габриэлевыми соседями.

Графы Габриэля естественным образом обобщаются на более высокие размерности, где пустые диски заменяются пустыми замкнутыми шарами. Названы в честь Рубена Габриэля, который ввёл их в совместной статье с Робертом Сокалом в 1969.