График Лайнвивера — Берка

График Лайнвивера — Берка, также Лайнуивера — Берка или график обратных двойных величин — графический метод представления уравнения Лайнвивера — Берка, характеризующее кинетику фермента. Используется в биохимии и энзимологии. Впервые метод был описан Хансом Лайнвивером и Дином Берком в 1934 году[1].

Пример графика Лайнвивера — Берка.

Для более удобного графического представления экспериментальных данных Лайнвивер и Берк преобразовали уравнение Бриггса — Холдейна (вывод уравнения Михаэлиса — Ментен) по методу двойных обратных величин исходя из того принципа, что если существует равенство между двумя какими-либо величинами, то и обратные величины также будут равны.

График Лайнуивера — Берка верен, когда кинетика фермента подчиняется кинетике идеальным реакциям второго порядка, однако нелинейная регрессия необходима для систем, которые не ведут себя идеально. Двойной обратный график искажает структуру ошибок данных и, следовательно, не является самым точным инструментом для определения кинетических параметров фермента. Для расчёта параметров обычно используются нелинейная регрессия или альтернативные линейные формы уравнения Михаэлиса — Ментен, такие как график Хейнса — Вульфа или график Иди — Хофсти[2].

Вывод

Графическое представление уравнения Лайнвивера — Берка — прямая, которая соответствует виду: y = ax + b. Преобразуем уравнение Михаэлиса — Ментен в линейную форму, для более удобного расчёта величин Vmax и Km. В частности если:

, то

которое и получило название уравнения Лайнвивера — Берка.

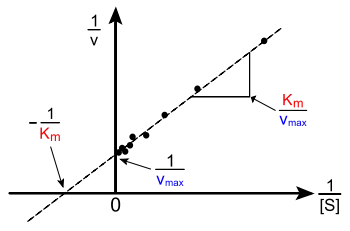
Теперь в соответствии с этим уравнением можно построить график в координатах 1/V (y) от 1/[S] (x)[3], при этом получим прямую линию, тангенс угла наклона который будет равен величине Km/Vmax; отрезок, отсекаемый прямой от оси ординат, представляет собой 1/Vmax (обратная величина максимальной скорости). Если продолжить прямую линию за ось ординат, тогда на абсциссе отсекается отрезок, соответствующий обратной величине константы Михаэлиса —1/Кm. Таким образом, величину Кm можно вычислить из данных наклона прямой и длины отрезка, отсекаемого от оси ординат, или из длины отрезка, отсекаемого от оси абсцисс в области отрицательных значений.

Примечания
  1. Lineweaver, Hans; Burk, Dean (March 1934). “The Determination of Enzyme Dissociation Constants”. Journal of the American Chemical Society [англ.]. 56 (3): 658—666. DOI:10.1021/ja01318a036. ISSN 0002-7863.
  2. Greco, W. R.; Hakala, M. T. (1979-12-10). “Evaluation of methods for estimating the dissociation constant of tight binding enzyme inhibitors”. The Journal of Biological Chemistry. 254 (23): 12104—12109. DOI:10.1016/S0021-9258(19)86435-9. ISSN 0021-9258. PMID 500698.
  3. Christensen, Siegfried B.; DeWolf, Walter E.; Ryan, M. Dominic & Torphy, Theodore J. (1996-01-01), Schudt, Christian; Dent, Gordon & Rabe, Klaus F., eds., 13 - Molecular Aspects of Inhibitor Interaction with PDE4, Handbook of Immunopharmacology, San Diego: Academic Press, с. 185–207, ISBN 978-0-12-210720-7, doi:10.1016/b978-012210720-7/50015-0, <http://www.sciencedirect.com/science/article/pii/B9780122107207500150>. Проверено 15 декабря 2020.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.